How do SGD hyperparameters in natural training affect adversarial robustness?

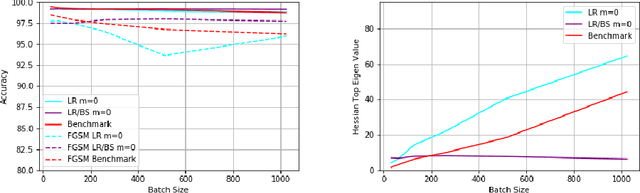
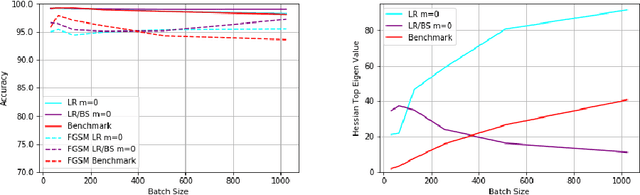
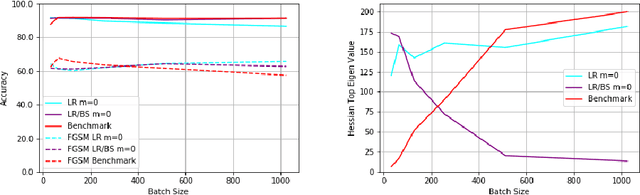
Learning rate, batch size and momentum are three important hyperparameters in the SGD algorithm. It is known from the work of Jastrzebski et al. arXiv:1711.04623 that large batch size training of neural networks yields models which do not generalize well. Yao et al. arXiv:1802.08241 observe that large batch training yields models that have poor adversarial robustness. In the same paper, the authors train models with different batch sizes and compute the eigenvalues of the Hessian of loss function. They observe that as the batch size increases, the dominant eigenvalues of the Hessian become larger. They also show that both adversarial training and small-batch training leads to a drop in the dominant eigenvalues of the Hessian or lowering its spectrum. They combine adversarial training and second order information to come up with a new large-batch training algorithm and obtain robust models with good generalization. In this paper, we empirically observe the effect of the SGD hyperparameters on the accuracy and adversarial robustness of networks trained with unperturbed samples. Jastrzebski et al. considered training models with a fixed learning rate to batch size ratio. They observed that higher the ratio, better is the generalization. We observe that networks trained with constant learning rate to batch size ratio, as proposed in Jastrzebski et al., yield models which generalize well and also have almost constant adversarial robustness, independent of the batch size. We observe that momentum is more effective with varying batch sizes and a fixed learning rate than with constant learning rate to batch size ratio based SGD training.

On Universalized Adversarial and Invariant Perturbations

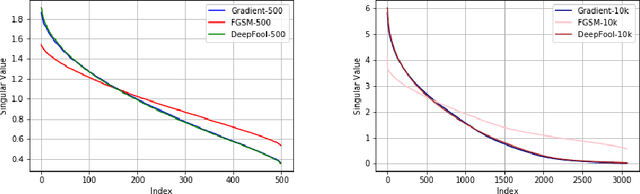
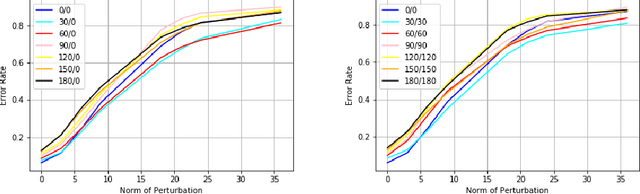
Convolutional neural networks or standard CNNs (StdCNNs) are translation-equivariant models that achieve translation invariance when trained on data augmented with sufficient translations. Recent work on equivariant models for a given group of transformations (e.g., rotations) has lead to group-equivariant convolutional neural networks (GCNNs). GCNNs trained on data augmented with sufficient rotations achieve rotation invariance. Recent work by authors arXiv:2002.11318 studies a trade-off between invariance and robustness to adversarial attacks. In another related work arXiv:2005.08632, given any model and any input-dependent attack that satisfies a certain spectral property, the authors propose a universalization technique called SVD-Universal to produce a universal adversarial perturbation by looking at very few test examples. In this paper, we study the effectiveness of SVD-Universal on GCNNs as they gain rotation invariance through higher degree of training augmentation. We empirically observe that as GCNNs gain rotation invariance through training augmented with larger rotations, the fooling rate of SVD-Universal gets better. To understand this phenomenon, we introduce universal invariant directions and study their relation to the universal adversarial direction produced by SVD-Universal.

Universalization of any adversarial attack using very few test examples

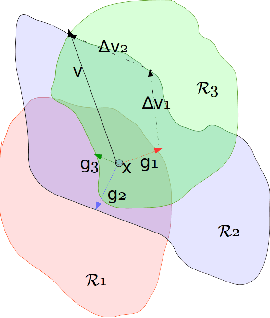
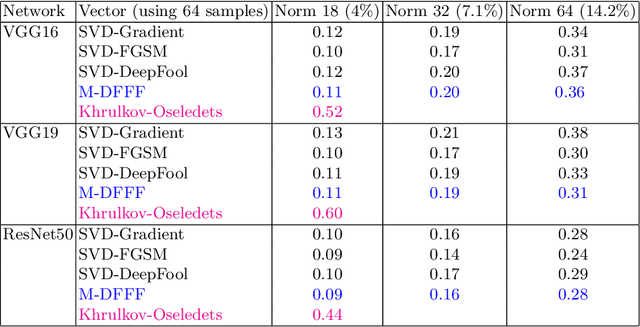
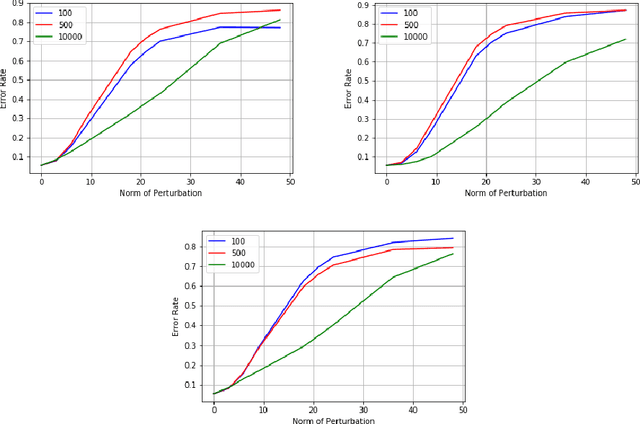
Deep learning models are known to be vulnerable not only to input-dependent adversarial attacks but also to input-agnostic or universal adversarial attacks. Dezfooli et al. \cite{Dezfooli17,Dezfooli17anal} construct universal adversarial attack on a given model by looking at a large number of training data points and the geometry of the decision boundary near them. Subsequent work \cite{Khrulkov18} constructs universal attack by looking only at test examples and intermediate layers of the given model. In this paper, we propose a simple universalization technique to take any input-dependent adversarial attack and construct a universal attack by only looking at very few adversarial test examples. We do not require details of the given model and have negligible computational overhead for universalization. We theoretically justify our universalization technique by a spectral property common to many input-dependent adversarial perturbations, e.g., gradients, Fast Gradient Sign Method (FGSM) and DeepFool. Using matrix concentration inequalities and spectral perturbation bounds, we show that the top singular vector of input-dependent adversarial directions on a small test sample gives an effective and simple universal adversarial attack. For VGG16 and VGG19 models trained on ImageNet, our simple universalization of Gradient, FGSM, and DeepFool perturbations using a test sample of 64 images gives fooling rates comparable to state-of-the-art universal attacks \cite{Dezfooli17,Khrulkov18} for reasonable norms of perturbation.

Invariance vs. Robustness of Neural Networks

We study the performance of neural network models on random geometric transformations and adversarial perturbations. Invariance means that the model's prediction remains unchanged when a geometric transformation is applied to an input. Adversarial robustness means that the model's prediction remains unchanged after small adversarial perturbations of an input. In this paper, we show a quantitative trade-off between rotation invariance and robustness. We empirically study the following two cases: (a) change in adversarial robustness as we improve only the invariance of equivariant models via training augmentation, (b) change in invariance as we improve only the adversarial robustness using adversarial training. We observe that the rotation invariance of equivariant models (StdCNNs and GCNNs) improves by training augmentation with progressively larger random rotations but while doing so, their adversarial robustness drops progressively, and very significantly on MNIST. We take adversarially trained LeNet and ResNet models which have good $L_\infty$ adversarial robustness on MNIST and CIFAR-10, respectively, and observe that adversarial training with progressively larger perturbations results in a progressive drop in their rotation invariance profiles. Similar to the trade-off between accuracy and robustness known in previous work, we give a theoretical justification for the invariance vs. robustness trade-off observed in our experiments.