Justin Ruths
Convex Optimization-based Policy Adaptation to Compensate for Distributional Shifts
Apr 05, 2023Abstract:Many real-world systems often involve physical components or operating environments with highly nonlinear and uncertain dynamics. A number of different control algorithms can be used to design optimal controllers for such systems, assuming a reasonably high-fidelity model of the actual system. However, the assumptions made on the stochastic dynamics of the model when designing the optimal controller may no longer be valid when the system is deployed in the real-world. The problem addressed by this paper is the following: Suppose we obtain an optimal trajectory by solving a control problem in the training environment, how do we ensure that the real-world system trajectory tracks this optimal trajectory with minimal amount of error in a deployment environment. In other words, we want to learn how we can adapt an optimal trained policy to distribution shifts in the environment. Distribution shifts are problematic in safety-critical systems, where a trained policy may lead to unsafe outcomes during deployment. We show that this problem can be cast as a nonlinear optimization problem that could be solved using heuristic method such as particle swarm optimization (PSO). However, if we instead consider a convex relaxation of this problem, we can learn policies that track the optimal trajectory with much better error performance, and faster computation times. We demonstrate the efficacy of our approach on tracking an optimal path using a Dubin's car model, and collision avoidance using both a linear and nonlinear model for adaptive cruise control.
Hybrid Zonotopes Exactly Represent ReLU Neural Networks
Apr 05, 2023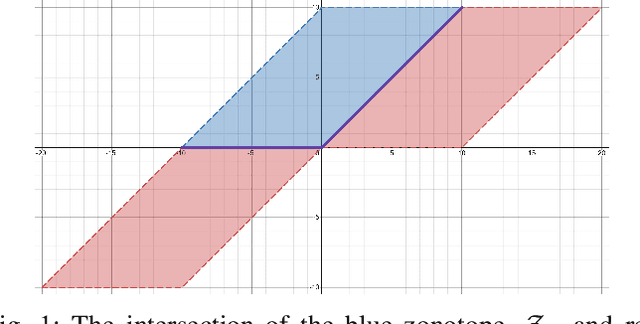
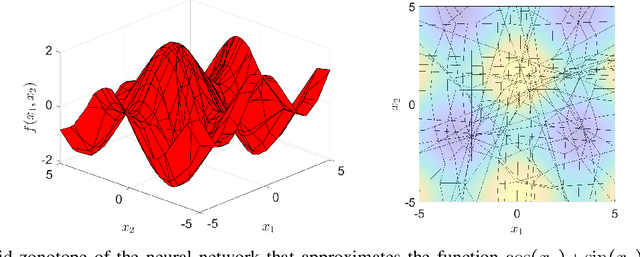
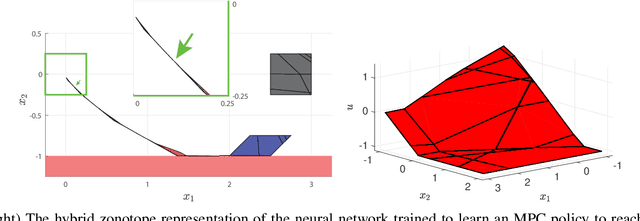
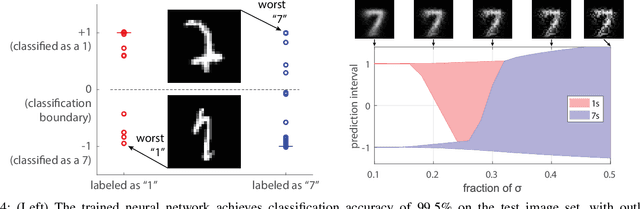
Abstract:We show that hybrid zonotopes offer an equivalent representation of feed-forward fully connected neural networks with ReLU activation functions. Our approach demonstrates that the complexity of binary variables is equal to the total number of neurons in the network and hence grows linearly in the size of the network. We demonstrate the utility of the hybrid zonotope formulation through three case studies including nonlinear function approximation, MPC closed-loop reachability and verification, and robustness of classification on the MNIST dataset.
Performance Bounds for Neural Network Estimators: Applications in Fault Detection
Mar 22, 2021
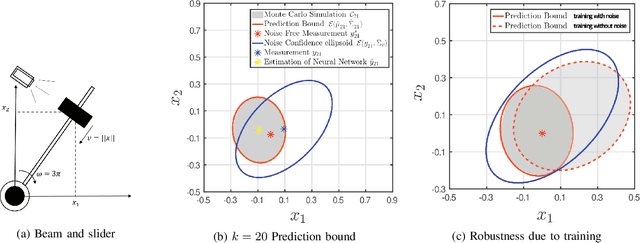

Abstract:We exploit recent results in quantifying the robustness of neural networks to input variations to construct and tune a model-based anomaly detector, where the data-driven estimator model is provided by an autoregressive neural network. In tuning, we specifically provide upper bounds on the rate of false alarms expected under normal operation. To accomplish this, we provide a theory extension to allow for the propagation of multiple confidence ellipsoids through a neural network. The ellipsoid that bounds the output of the neural network under the input variation informs the sensitivity - and thus the threshold tuning - of the detector. We demonstrate this approach on a linear and nonlinear dynamical system.
Certifying Incremental Quadratic Constraints for Neural Networks via Convex Optimization
Dec 19, 2020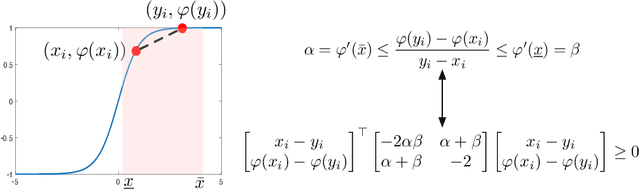
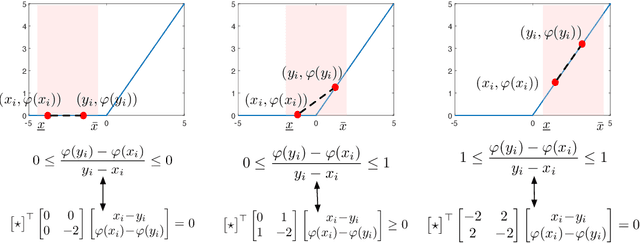
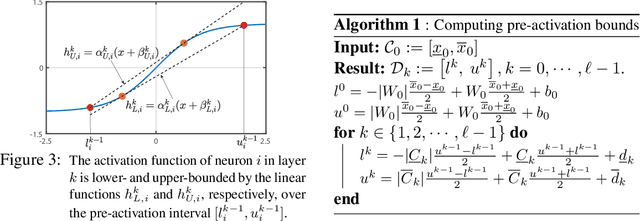
Abstract:Abstracting neural networks with constraints they impose on their inputs and outputs can be very useful in the analysis of neural network classifiers and to derive optimization-based algorithms for certification of stability and robustness of feedback systems involving neural networks. In this paper, we propose a convex program, in the form of a Linear Matrix Inequality (LMI), to certify incremental quadratic constraints on the map of neural networks over a region of interest. These certificates can capture several useful properties such as (local) Lipschitz continuity, one-sided Lipschitz continuity, invertibility, and contraction. We illustrate the utility of our approach in two different settings. First, we develop a semidefinite program to compute guaranteed and sharp upper bounds on the local Lipschitz constant of neural networks and illustrate the results on random networks as well as networks trained on MNIST. Second, we consider a linear time-invariant system in feedback with an approximate model predictive controller parameterized by a neural network. We then turn the stability analysis into a semidefinite feasibility program and estimate an ellipsoidal invariant set for the closed-loop system.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge