Unperturbed: spectral analysis beyond Davis-Kahan

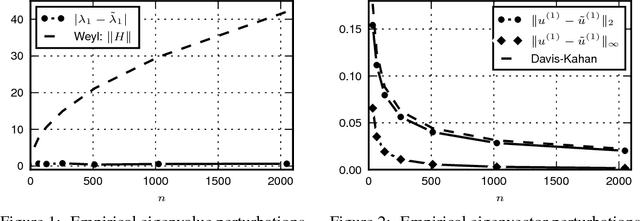
Classical matrix perturbation results, such as Weyl's theorem for eigenvalues and the Davis-Kahan theorem for eigenvectors, are general purpose. These classical bounds are tight in the worst case, but in many settings sub-optimal in the typical case. In this paper, we present perturbation bounds which consider the nature of the perturbation and its interaction with the unperturbed structure in order to obtain significant improvements over the classical theory in many scenarios, such as when the perturbation is random. We demonstrate the utility of these new results by analyzing perturbations in the stochastic blockmodel where we derive much tighter bounds than provided by the classical theory. We use our new perturbation theory to show that a very simple and natural clustering algorithm -- whose analysis was difficult using the classical tools -- nevertheless recovers the communities of the blockmodel exactly even in very sparse graphs.

Graphons, mergeons, and so on!

In this work we develop a theory of hierarchical clustering for graphs. Our modeling assumption is that graphs are sampled from a graphon, which is a powerful and general model for generating graphs and analyzing large networks. Graphons are a far richer class of graph models than stochastic blockmodels, the primary setting for recent progress in the statistical theory of graph clustering. We define what it means for an algorithm to produce the "correct" clustering, give sufficient conditions in which a method is statistically consistent, and provide an explicit algorithm satisfying these properties.

Beyond Hartigan Consistency: Merge Distortion Metric for Hierarchical Clustering

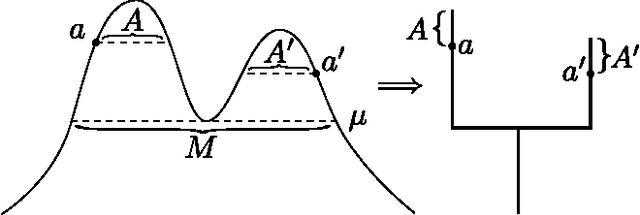
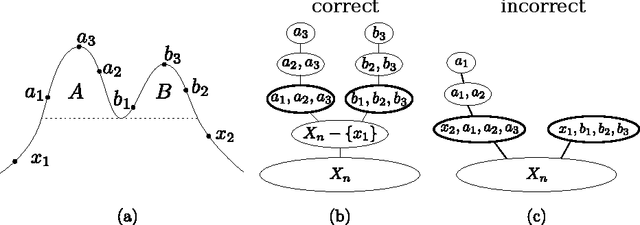
Hierarchical clustering is a popular method for analyzing data which associates a tree to a dataset. Hartigan consistency has been used extensively as a framework to analyze such clustering algorithms from a statistical point of view. Still, as we show in the paper, a tree which is Hartigan consistent with a given density can look very different than the correct limit tree. Specifically, Hartigan consistency permits two types of undesirable configurations which we term over-segmentation and improper nesting. Moreover, Hartigan consistency is a limit property and does not directly quantify difference between trees. In this paper we identify two limit properties, separation and minimality, which address both over-segmentation and improper nesting and together imply (but are not implied by) Hartigan consistency. We proceed to introduce a merge distortion metric between hierarchical clusterings and show that convergence in our distance implies both separation and minimality. We also prove that uniform separation and minimality imply convergence in the merge distortion metric. Furthermore, we show that our merge distortion metric is stable under perturbations of the density. Finally, we demonstrate applicability of these concepts by proving convergence results for two clustering algorithms. First, we show convergence (and hence separation and minimality) of the recent robust single linkage algorithm of Chaudhuri and Dasgupta (2010). Second, we provide convergence results on manifolds for topological split tree clustering.