Tailoring the Hyperparameters of a Wide-Kernel Convolutional Neural Network to Fit Different Bearing Fault Vibration Datasets

State-of-the-art algorithms are reported to be almost perfect at distinguishing the vibrations arising from healthy and damaged machine bearings, according to benchmark datasets at least. However, what about their application to new data? In this paper, we are able to confirm that neural networks for bearing fault detection can be crippled by incorrect hyperparameterisation, and also that the correct hyperparameter settings can actually change when transitioning to new data. The paper weaves together multiple methods to explain the behaviour of the hyperparameters of a wide-kernel convolutional neural network and how to set them. Since guidance already exists for generic hyperparameters like minibatch size, we focus on how to set architecture-specific hyperparameters such as the width of the convolutional kernels, a topic which might otherwise be obscure. We reflect different data properties by fusing information from seven different benchmark datasets, and our results show that the kernel size in the first layer in particular is sensitive to changes in the data. Looking deeper, we use manipulated copies of one dataset in an attempt to spot why the kernel size sometimes needs to change. The relevance of sampling rate is studied by using different levels of resampling, and spectral content is studied by increasingly filtering out high frequencies. At the end of our paper we conclude by stating clear guidance on how to set the hyperparameters of our neural network architecture.

Multivariate Time Series Regression with Graph Neural Networks

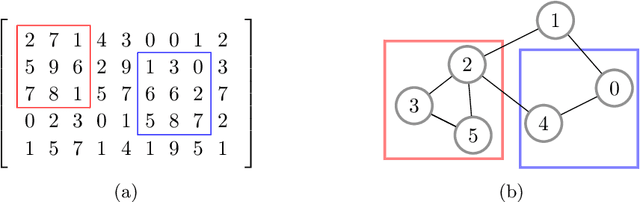
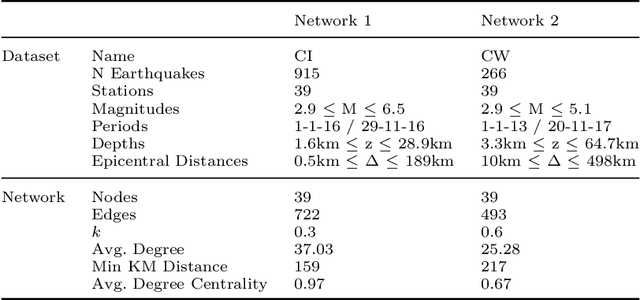
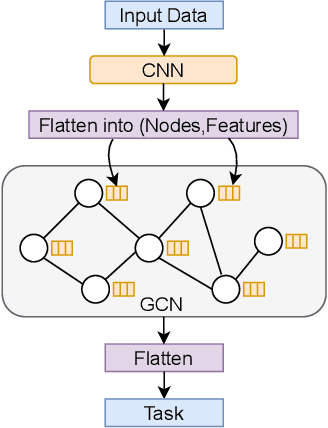
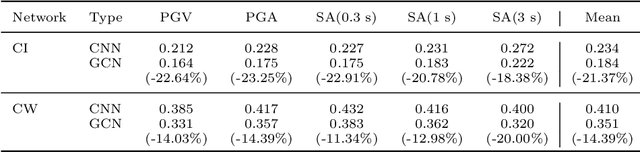
Machine learning, with its advances in Deep Learning has shown great potential in analysing time series in the past. However, in many scenarios, additional information is available that can potentially improve predictions, by incorporating it into the learning methods. This is crucial for data that arises from e.g., sensor networks that contain information about sensor locations. Then, such spatial information can be exploited by modeling it via graph structures, along with the sequential (time) information. Recent advances in adapting Deep Learning to graphs have shown promising potential in various graph-related tasks. However, these methods have not been adapted for time series related tasks to a great extent. Specifically, most attempts have essentially consolidated around Spatial-Temporal Graph Neural Networks for time series forecasting with small sequence lengths. Generally, these architectures are not suited for regression or classification tasks that contain large sequences of data. Therefore, in this work, we propose an architecture capable of processing these long sequences in a multivariate time series regression task, using the benefits of Graph Neural Networks to improve predictions. Our model is tested on two seismic datasets that contain earthquake waveforms, where the goal is to predict intensity measurements of ground shaking at a set of stations. Our findings demonstrate promising results of our approach, which are discussed in depth with an additional ablation study.

A Computational Framework for Modeling Complex Sensor Network Data Using Graph Signal Processing and Graph Neural Networks in Structural Health Monitoring

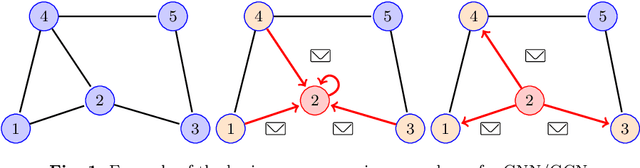
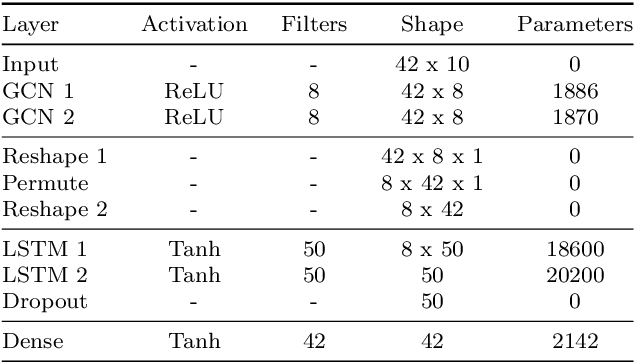
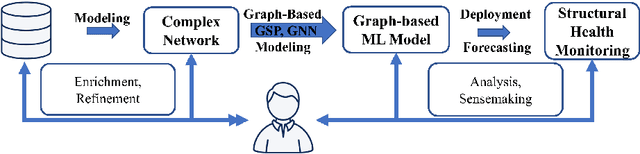
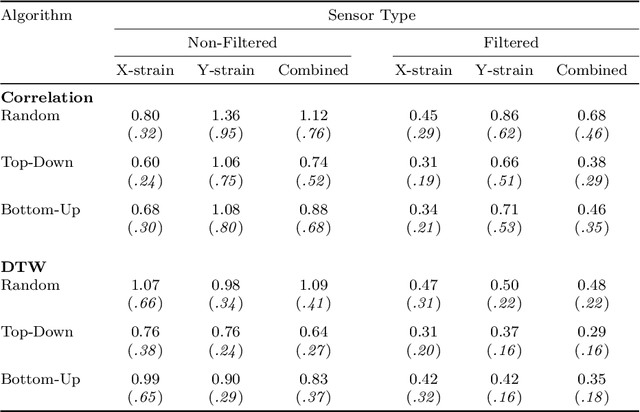
Complex networks lend themselves to the modeling of multidimensional data, such as relational and/or temporal data. In particular, when such complex data and their inherent relationships need to be formalized, complex network modeling and its resulting graph representations enable a wide range of powerful options. In this paper, we target this - connected to specific machine learning approaches on graphs for structural health monitoring on an analysis and predictive (maintenance) perspective. Specifically, we present a framework based on Complex Network Modeling, integrating Graph Signal Processing (GSP) and Graph Neural Network (GNN) approaches. We demonstrate this framework in our targeted application domain of Structural Health Monitoring (SHM). In particular, we focus on a prominent real-world structural health monitoring use case, i.e., modeling and analyzing sensor data (strain, vibration) of a large bridge in the Netherlands. In our experiments, we show that GSP enables the identification of the most important sensors, for which we investigate a set of search and optimization approaches. Furthermore, GSP enables the detection of specific graph signal patterns (mode shapes), capturing physical functional properties of the sensors in the applied complex network. In addition, we show the efficacy of applying GNNs for strain prediction on this kind of data.