A Neural Dirichlet Process Mixture Model for Task-Free Continual Learning

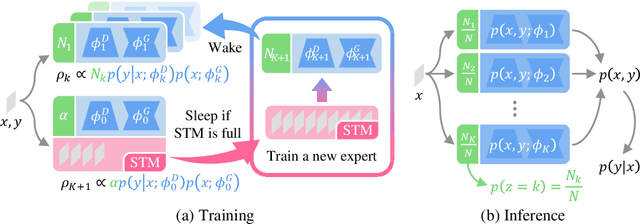
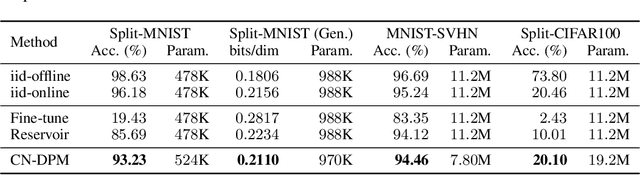
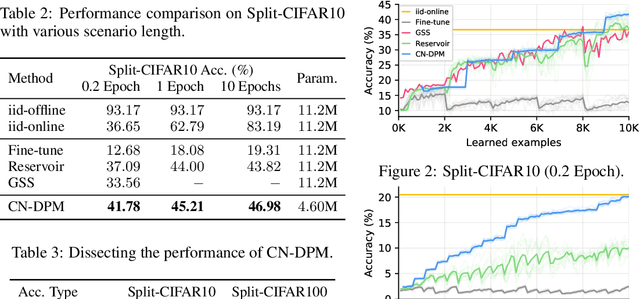
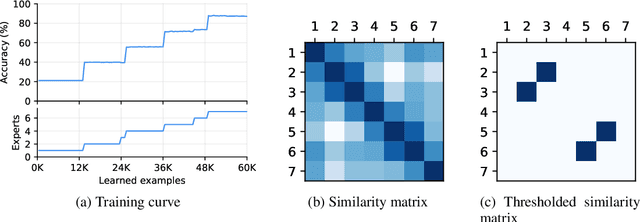
Despite the growing interest in continual learning, most of its contemporary works have been studied in a rather restricted setting where tasks are clearly distinguishable, and task boundaries are known during training. However, if our goal is to develop an algorithm that learns as humans do, this setting is far from realistic, and it is essential to develop a methodology that works in a task-free manner. Meanwhile, among several branches of continual learning, expansion-based methods have the advantage of eliminating catastrophic forgetting by allocating new resources to learn new data. In this work, we propose an expansion-based approach for task-free continual learning. Our model, named Continual Neural Dirichlet Process Mixture (CN-DPM), consists of a set of neural network experts that are in charge of a subset of the data. CN-DPM expands the number of experts in a principled way under the Bayesian nonparametric framework. With extensive experiments, we show that our model successfully performs task-free continual learning for both discriminative and generative tasks such as image classification and image generation.

Harmonizing Maximum Likelihood with GANs for Multimodal Conditional Generation

Recent advances in conditional image generation tasks, such as image-to-image translation and image inpainting, are largely accounted to the success of conditional GAN models, which are often optimized by the joint use of the GAN loss with the reconstruction loss. However, we reveal that this training recipe shared by almost all existing methods causes one critical side effect: lack of diversity in output samples. In order to accomplish both training stability and multimodal output generation, we propose novel training schemes with a new set of losses named moment reconstruction losses that simply replace the reconstruction loss. We show that our approach is applicable to any conditional generation tasks by performing thorough experiments on image-to-image translation, super-resolution and image inpainting using Cityscapes and CelebA dataset. Quantitative evaluations also confirm that our methods achieve a great diversity in outputs while retaining or even improving the visual fidelity of generated samples.