Auxiliary-Tasks Learning for Physics-Informed Neural Network-Based Partial Differential Equations Solving

Physics-informed neural networks (PINNs) have emerged as promising surrogate modes for solving partial differential equations (PDEs). Their effectiveness lies in the ability to capture solution-related features through neural networks. However, original PINNs often suffer from bottlenecks, such as low accuracy and non-convergence, limiting their applicability in complex physical contexts. To alleviate these issues, we proposed auxiliary-task learning-based physics-informed neural networks (ATL-PINNs), which provide four different auxiliary-task learning modes and investigate their performance compared with original PINNs. We also employ the gradient cosine similarity algorithm to integrate auxiliary problem loss with the primary problem loss in ATL-PINNs, which aims to enhance the effectiveness of the auxiliary-task learning modes. To the best of our knowledge, this is the first study to introduce auxiliary-task learning modes in the context of physics-informed learning. We conduct experiments on three PDE problems across different fields and scenarios. Our findings demonstrate that the proposed auxiliary-task learning modes can significantly improve solution accuracy, achieving a maximum performance boost of 96.62% (averaging 28.23%) compared to the original single-task PINNs. The code and dataset are open source at https://github.com/junjun-yan/ATL-PINN.

ST-PINN: A Self-Training Physics-Informed Neural Network for Partial Differential Equations

Partial differential equations (PDEs) are an essential computational kernel in physics and engineering. With the advance of deep learning, physics-informed neural networks (PINNs), as a mesh-free method, have shown great potential for fast PDE solving in various applications. To address the issue of low accuracy and convergence problems of existing PINNs, we propose a self-training physics-informed neural network, ST-PINN. Specifically, ST-PINN introduces a pseudo label based self-learning algorithm during training. It employs governing equation as the pseudo-labeled evaluation index and selects the highest confidence examples from the sample points to attach the pseudo labels. To our best knowledge, we are the first to incorporate a self-training mechanism into physics-informed learning. We conduct experiments on five PDE problems in different fields and scenarios. The results demonstrate that the proposed method allows the network to learn more physical information and benefit convergence. The ST-PINN outperforms existing physics-informed neural network methods and improves the accuracy by a factor of 1.33x-2.54x. The code of ST-PINN is available at GitHub: https://github.com/junjun-yan/ST-PINN.

An Improved Structured Mesh Generation Method Based on Physics-informed Neural Networks

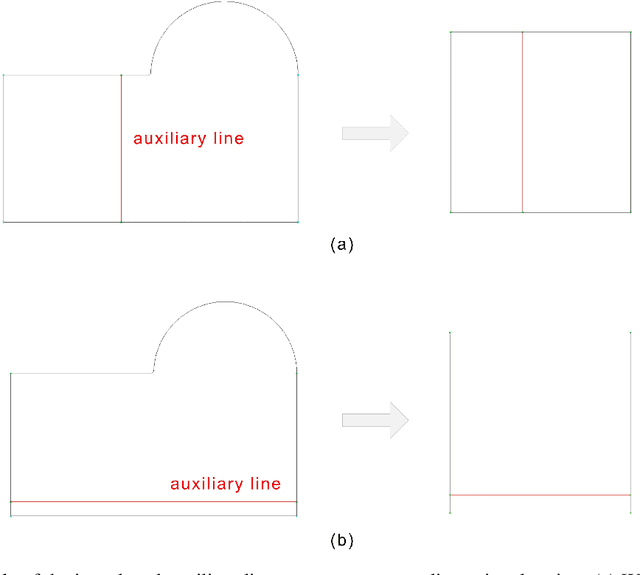
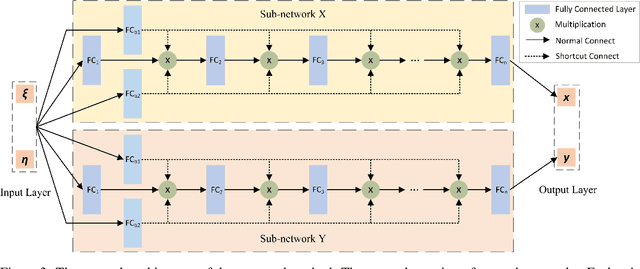
Mesh generation remains a key technology in many areas where numerical simulations are required. As numerical algorithms become more efficient and computers become more powerful, the percentage of time devoted to mesh generation becomes higher. In this paper, we present an improved structured mesh generation method. The method formulates the meshing problem as a global optimization problem related to a physics-informed neural network. The mesh is obtained by intelligently solving the physical boundary-constrained partial differential equations. To improve the prediction accuracy of the neural network, we also introduce a novel auxiliary line strategy and an efficient network model during meshing. The strategy first employs a priori auxiliary lines to provide ground truth data and then uses these data to construct a loss term to better constrain the convergence of the subsequent training. The experimental results indicate that the proposed method is effective and robust. It can accurately approximate the mapping (transformation) from the computational domain to the physical domain and enable fast high-quality structured mesh generation.