Multi-Step Embed to Control: A Novel Deep Learning-based Approach for Surrogate Modelling in Reservoir Simulation

Reduced-order models, also known as proxy model or surrogate model, are approximate models that are less computational expensive as opposed to fully descriptive models. With the integration of machine learning, these models have garnered increasing research interests recently. However, many existing reduced-order modeling methods, such as embed to control (E2C) and embed to control and observe (E2CO), fall short in long-term predictions due to the accumulation of prediction errors over time. This issue arises partly from the one-step prediction framework inherent in E2C and E2CO architectures. This paper introduces a deep learning-based surrogate model, referred as multi-step embed-to-control model, for the construction of proxy models with improved long-term prediction performance. Unlike E2C and E2CO, the proposed network considers multiple forward transitions in the latent space at a time using Koopman operator, allowing the model to incorporate a sequence of state snapshots during training phrases. Additionally, the loss function of this novel approach has been redesigned to accommodate these multiple transitions and to respect the underlying physical principles. To validate the efficacy of the proposed method, the developed framework was implemented within two-phase (oil and water) reservoir model under a waterflooding scheme. Comparative analysis demonstrate that the proposed model significantly outperforms the conventional E2C model in long-term simulation scenarios. Notably, there was a substantial reduction in temporal errors in the prediction of saturation profiles and a decent improvement in pressure forecasting accuracy.

Transfer learning-based physics-informed convolutional neural network for simulating flow in porous media with time-varying controls

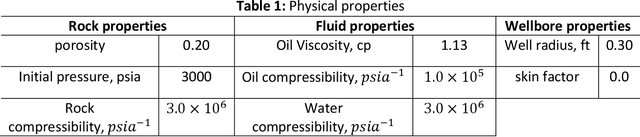
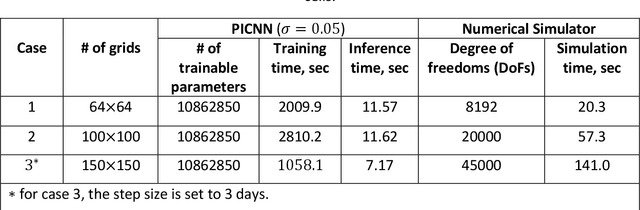
A physics-informed convolutional neural network is proposed to simulate two phase flow in porous media with time-varying well controls. While most of PICNNs in existing literatures worked on parameter-to-state mapping, our proposed network parameterizes the solution with time-varying controls to establish a control-to-state regression. Firstly, finite volume scheme is adopted to discretize flow equations and formulate loss function that respects mass conservation laws. Neumann boundary conditions are seamlessly incorporated into the semi-discretized equations so no additional loss term is needed. The network architecture comprises two parallel U-Net structures, with network inputs being well controls and outputs being the system states. To capture the time-dependent relationship between inputs and outputs, the network is well designed to mimic discretized state space equations. We train the network progressively for every timestep, enabling it to simultaneously predict oil pressure and water saturation at each timestep. After training the network for one timestep, we leverage transfer learning techniques to expedite the training process for subsequent timestep. The proposed model is used to simulate oil-water porous flow scenarios with varying reservoir gridblocks and aspects including computation efficiency and accuracy are compared against corresponding numerical approaches. The results underscore the potential of PICNN in effectively simulating systems with numerous grid blocks, as computation time does not scale with model dimensionality. We assess the temporal error using 10 different testing controls with variation in magnitude and another 10 with higher alternation frequency with proposed control-to-state architecture. Our observations suggest the need for a more robust and reliable model when dealing with controls that exhibit significant variations in magnitude or frequency.

Physics-informed Convolutional Recurrent Surrogate Model for Reservoir Simulation with Well Controls

This paper presents a novel surrogate model for modeling subsurface fluid flow with well controls using a physics-informed convolutional recurrent neural network (PICRNN). The model uses a convolutional long-short term memory (ConvLSTM) to capture the spatiotemporal dependencies of the state evolution dynamics in the porous flow. The ConvLSTM is linked to the state space equations, enabling the incorporation of a discrete-time sequence of well control. The model requires initial state condition and a sequence of well controls as inputs, and predicts the state variables of the system, such as pressure, as output. By minimizing the residuals of reservoir flow state-space equations, the network is trained without the need for labeled data. The model is designed to serve as a surrogate model for predicting future reservoir states based on the initial reservoir state and input engineering controls. Boundary conditions are enforced into the state-space equations so no additional loss term is needed. Three numerical cases are studied, demonstrating the model's effectiveness in predicting reservoir dynamics based on future well/system controls. The proposed model provides a new approach for efficient and accurate prediction of subsurface fluid flow, with potential applications in optimal control design for reservoir engineering.