Fast and Robust Fixed-Rank Matrix Recovery

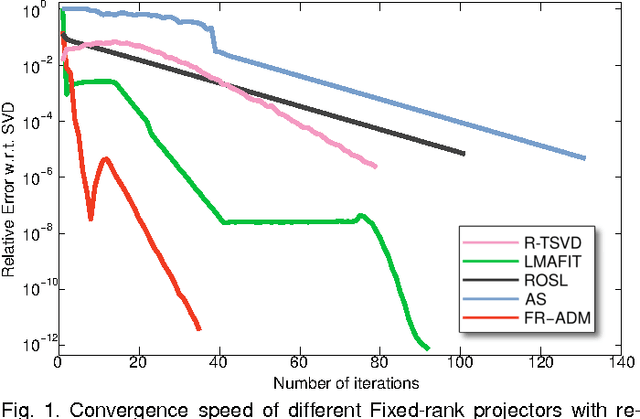
We address the problem of efficient sparse fixed-rank (S-FR) matrix decomposition, i.e., splitting a corrupted matrix $M$ into an uncorrupted matrix $L$ of rank $r$ and a sparse matrix of outliers $S$. Fixed-rank constraints are usually imposed by the physical restrictions of the system under study. Here we propose a method to perform accurate and very efficient S-FR decomposition that is more suitable for large-scale problems than existing approaches. Our method is a grateful combination of geometrical and algebraical techniques, which avoids the bottleneck caused by the Truncated SVD (TSVD). Instead, a polar factorization is used to exploit the manifold structure of fixed-rank problems as the product of two Stiefel and an SPD manifold, leading to a better convergence and stability. Then, closed-form projectors help to speed up each iteration of the method. We introduce a novel and fast projector for the $\text{SPD}$ manifold and a proof of its validity. Further acceleration is achieved using a Nystrom scheme. Extensive experiments with synthetic and real data in the context of robust photometric stereo and spectral clustering show that our proposals outperform the state of the art.

Motion Estimation via Robust Decomposition with Constrained Rank

In this work, we address the problem of outlier detection for robust motion estimation by using modern sparse-low-rank decompositions, i.e., Robust PCA-like methods, to impose global rank constraints. Robust decompositions have shown to be good at splitting a corrupted matrix into an uncorrupted low-rank matrix and a sparse matrix, containing outliers. However, this process only works when matrices have relatively low rank with respect to their ambient space, a property not met in motion estimation problems. As a solution, we propose to exploit the partial information present in the decomposition to decide which matches are outliers. We provide evidences showing that even when it is not possible to recover an uncorrupted low-rank matrix, the resulting information can be exploited for outlier detection. To this end we propose the Robust Decomposition with Constrained Rank (RD-CR), a proximal gradient based method that enforces the rank constraints inherent to motion estimation. We also present a general framework to perform robust estimation for stereo Visual Odometry, based on our RD-CR and a simple but effective compressed optimization method that achieves high performance. Our evaluation on synthetic data and on the KITTI dataset demonstrates the applicability of our approach in complex scenarios and it yields state-of-the-art performance.