Statistical Properties of the Entropy from Ordinal Patterns

The ultimate purpose of the statistical analysis of ordinal patterns is to characterize the distribution of the features they induce. In particular, knowing the joint distribution of the pair Entropy-Statistical Complexity for a large class of time series models would allow statistical tests that are unavailable to date. Working in this direction, we characterize the asymptotic distribution of the empirical Shannon's Entropy for any model under which the true normalized Entropy is neither zero nor one. We obtain the asymptotic distribution from the Central Limit Theorem (assuming large time series), the Multivariate Delta Method, and a third-order correction of its mean value. We discuss the applicability of other results (exact, first-, and second-order corrections) regarding their accuracy and numerical stability. Within a general framework for building test statistics about Shannon's Entropy, we present a bilateral test that verifies if there is enough evidence to reject the hypothesis that two signals produce ordinal patterns with the same Shannon's Entropy. We applied this bilateral test to the daily maximum temperature time series from three cities (Dublin, Edinburgh, and Miami) and obtained sensible results.

Comparing Samples from the $\mathcal{G}^0$ Distribution using a Geodesic Distance

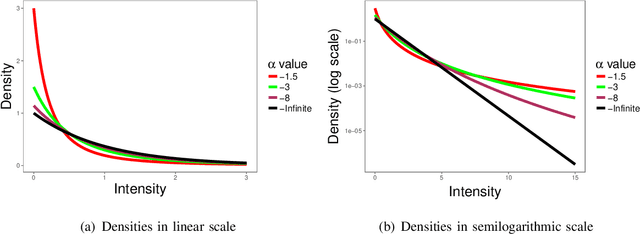
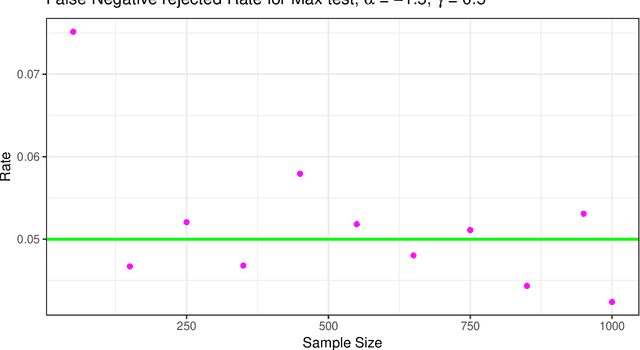
The $\mathcal{G}^0$ distribution is widely used for monopolarized SAR image modeling because it can characterize regions with different degree of texture accurately. It is indexed by three parameters: the number of looks (which can be estimated for the whole image), a scale parameter and a texture parameter. This paper presents a new proposal for comparing samples from the $\mathcal{G}^0$ distribution using a Geodesic Distance (GD) as a measure of dissimilarity between models. The objective is quantifying the difference between pairs of samples from SAR data using both local parameters (scale and texture) of the $\mathcal{G}^0$ distribution. We propose three tests based on the GD which combine the tests presented in~\cite{GeodesicDistanceGI0JSTARS}, and we estimate their probability distributions using permutation methods.

Parameter Estimation for the Single-Look $\mathcal{G}^0$ Distribution

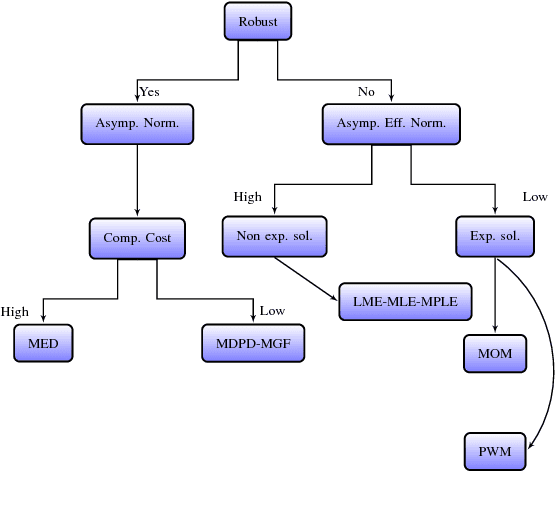
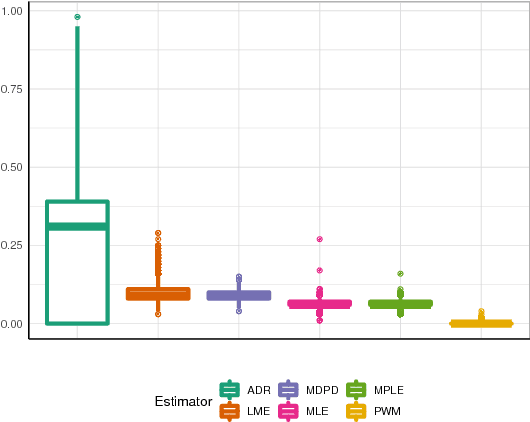
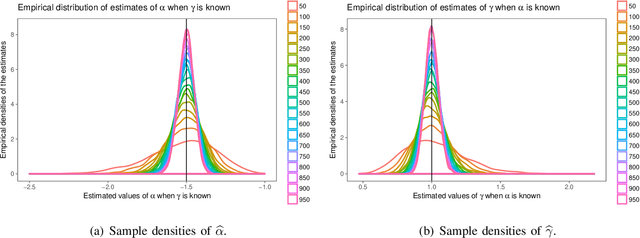
The statistical properties of Synthetic Aperture Radar (SAR) image texture reveals useful target characteristics. It is well-known that these images are affected by speckle, and prone to contamination as double bounce and corner reflectors. The $\mathcal{G}^0$ distribution is flexible enough to model different degrees of texture in speckled data. It is indexed by three parameters: $\alpha$, related to the texture, $\gamma$, a scale parameter, and $L$, the number of looks which is related to the signal-to-noise ratio. Quality estimation of $\alpha$ is essential due to its immediate interpretability. In this article, we compare the behavior of a number of parameter estimation techniques in the noisiest case, namely single look data. We evaluate them using Monte Carlo methods for non-contaminated and contaminated data, considering convergence rate, bias, mean squared error (MSE) and computational cost. The results are verified with simulated and actual SAR images.

The Geodesic Distance between $\mathcal{G}_I^0$ Models and its Application to Region Discrimination

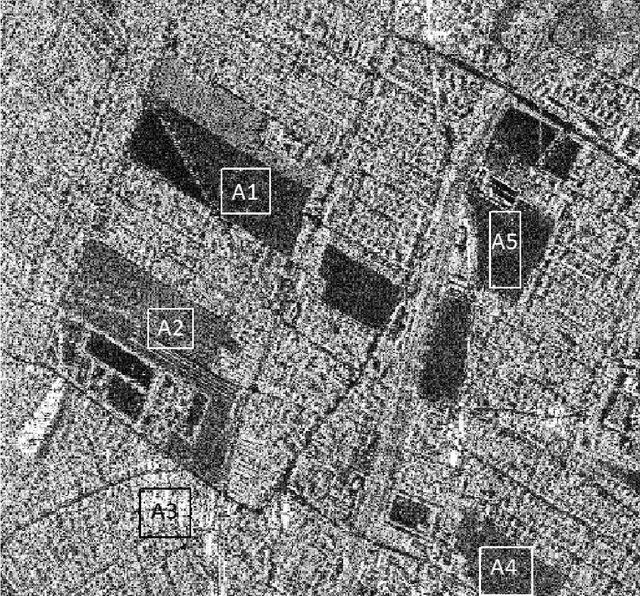
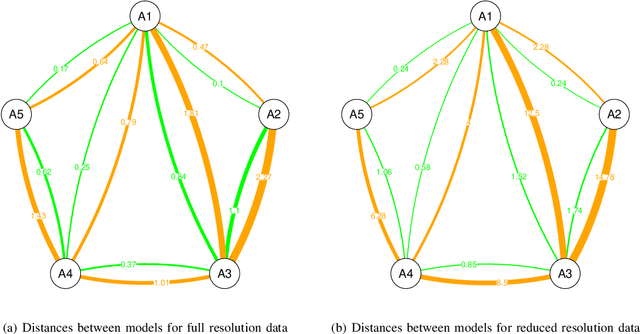
The $\mathcal{G}_I^0$ distribution is able to characterize different regions in monopolarized SAR imagery. It is indexed by three parameters: the number of looks (which can be estimated in the whole image), a scale parameter and a texture parameter. This paper presents a new proposal for feature extraction and region discrimination in SAR imagery, using the geodesic distance as a measure of dissimilarity between $\mathcal{G}_I^0$ models. We derive geodesic distances between models that describe several practical situations, assuming the number of looks known, for same and different texture and for same and different scale. We then apply this new tool to the problems of (i)~identifying edges between regions with different texture, and (ii)~quantify the dissimilarity between pairs of samples in actual SAR data. We analyze the advantages of using the geodesic distance when compared to stochastic distances.

Fast Cosine Transform to increase speed-up and efficiency of Karhunen-Loeve Transform for lossy image compression

In this work, we present a comparison between two techniques of image compression. In the first case, the image is divided in blocks which are collected according to zig-zag scan. In the second one, we apply the Fast Cosine Transform to the image, and then the transformed image is divided in blocks which are collected according to zig-zag scan too. Later, in both cases, the Karhunen-Loeve transform is applied to mentioned blocks. On the other hand, we present three new metrics based on eigenvalues for a better comparative evaluation of the techniques. Simulations show that the combined version is the best, with minor Mean Absolute Error (MAE) and Mean Squared Error (MSE), higher Peak Signal to Noise Ratio (PSNR) and better image quality. Finally, new technique was far superior to JPEG and JPEG2000.

Polarimetric SAR Image Segmentation with B-Splines and a New Statistical Model

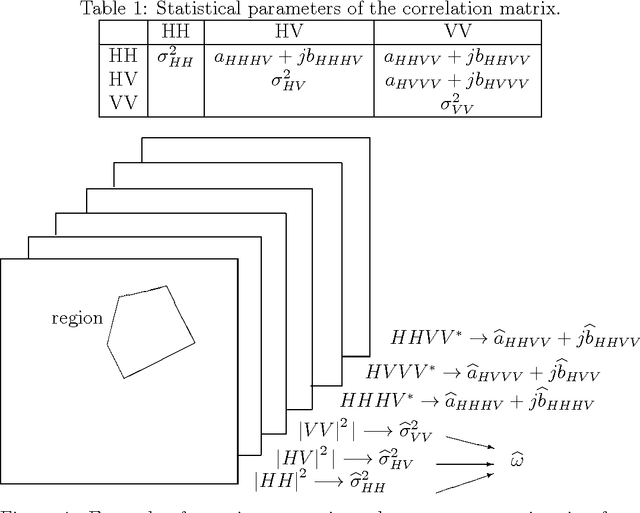
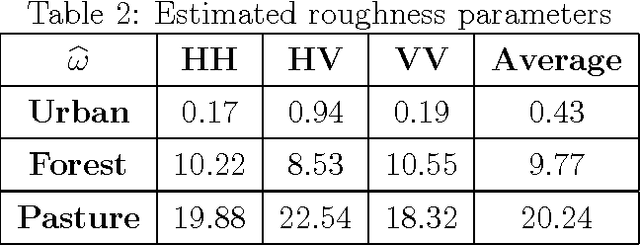
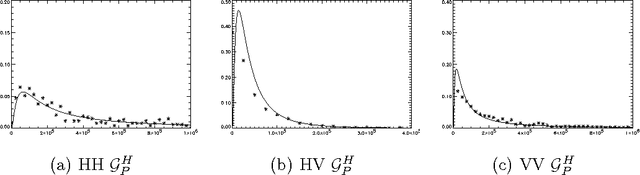
We present an approach for polarimetric Synthetic Aperture Radar (SAR) image region boundary detection based on the use of B-Spline active contours and a new model for polarimetric SAR data: the GHP distribution. In order to detect the boundary of a region, initial B-Spline curves are specified, either automatically or manually, and the proposed algorithm uses a deformable contours technique to find the boundary. In doing this, the parameters of the polarimetric GHP model for the data are estimated, in order to find the transition points between the region being segmented and the surrounding area. This is a local algorithm since it works only on the region to be segmented. Results of its performance are presented.