Quantum spectral analysis: frequency in time, with applications to signal and image processing

A quantum time-dependent spectrum analysis, or simply, quantum spectral analysis (QSA) is presented in this work, and it is based on Schrodinger equation, which is a partial differential equation that describes how the quantum state of a non-relativistic physical system changes with time. In classic world is named frequency in time (FIT), which is presented here in opposition and as a complement of traditional spectral analysis frequency-dependent based on Fourier theory. Besides, FIT is a metric, which assesses the impact of the flanks of a signal on its frequency spectrum, which is not taken into account by Fourier theory and even less in real time. Even more, and unlike all derived tools from Fourier Theory (i.e., continuous, discrete, fast, short-time, fractional and quantum Fourier Transform, as well as, Gabor) FIT has the following advantages: a) compact support with excellent energy output treatment, b) low computational cost, O(N) for signals and O(N2) for images, c) it does not have phase uncertainties (indeterminate phase for magnitude = 0) as Discrete and Fast Fourier Transform (DFT, FFT, respectively), d) among others. In fact, FIT constitutes one side of a triangle (which from now on is closed) and it consists of the original signal in time, spectral analysis based on Fourier Theory and FIT. Thus a toolbox is completed, which it is essential for all applications of Digital Signal Processing (DSP) and Digital Image Processing (DIP); and, even, in the latter, FIT allows edge detection (which is called flank detection in case of signals), denoising, despeckling, compression, and superresolution of still images. Such applications include signals intelligence and imagery intelligence. On the other hand, we will present other DIP tools, which are also derived from the Schrodinger equation.

Enhanced Directional Smoothing Algorithm for Edge-Preserving Smoothing of Synthetic-Aperture Radar Images

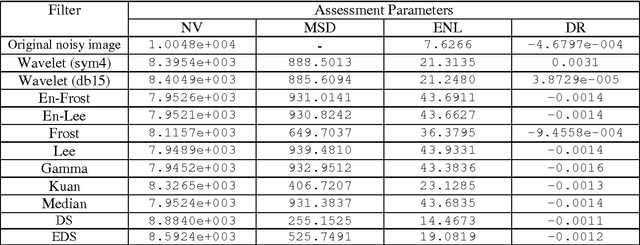
Synthetic aperture radar (SAR) images are subject to prominent speckle noise, which is generally considered a purely multiplicative noise process. In theory, this multiplicative noise is that the ratio of the standard deviation to the signal value, the "coefficient of variation," is theoretically constant at every point in a SAR image. Most of the filters for speckle reduction are based on this property. Such property is irrelevant for the new filter structure, which is based on directional smoothing (DS) theory, the enhanced directional smoothing (EDS) that removes speckle noise from SAR images without blurring edges. We demonstrate the effectiveness of this new filtering method by comparing it to established speckle noise removal techniques on SAR images.

Neural shrinkage for wavelet-based SAR despeckling

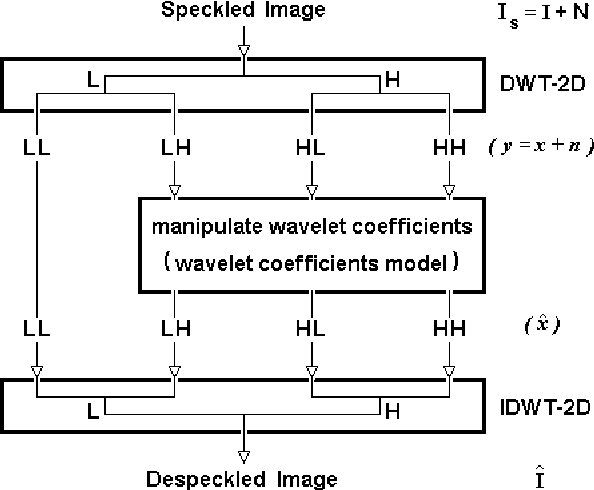
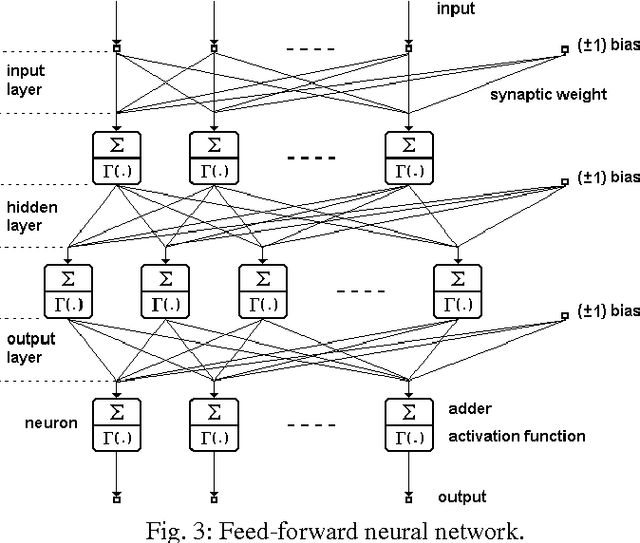
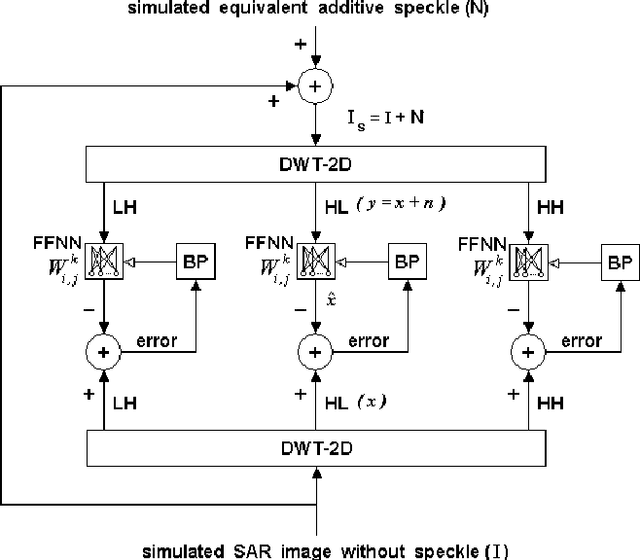
The wavelet shrinkage denoising approach is able to maintain local regularity of a signal while suppressing noise. However, the conventional wavelet shrinkage based methods are not time-scale adaptive to track the local time-scale variation. In this paper, a new type of Neural Shrinkage (NS) is presented with a new class of shrinkage architecture for speckle reduction in Synthetic Aperture Radar (SAR) images. The numerical results indicate that the new method outperforms the standard filters, the standard wavelet shrinkage despeckling method, and previous NS.

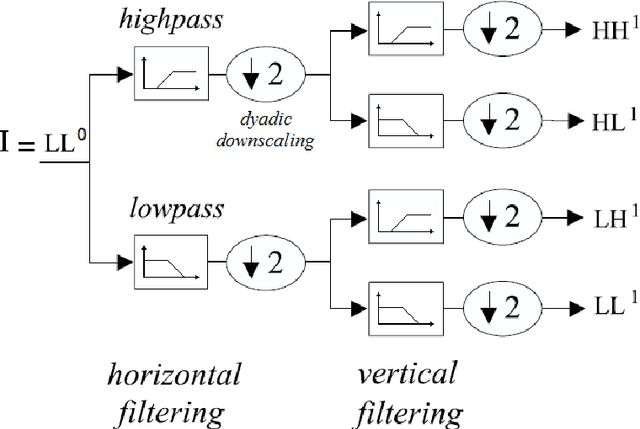
Fuzzy thresholding in wavelet domain for speckle reduction in Synthetic Aperture Radar images

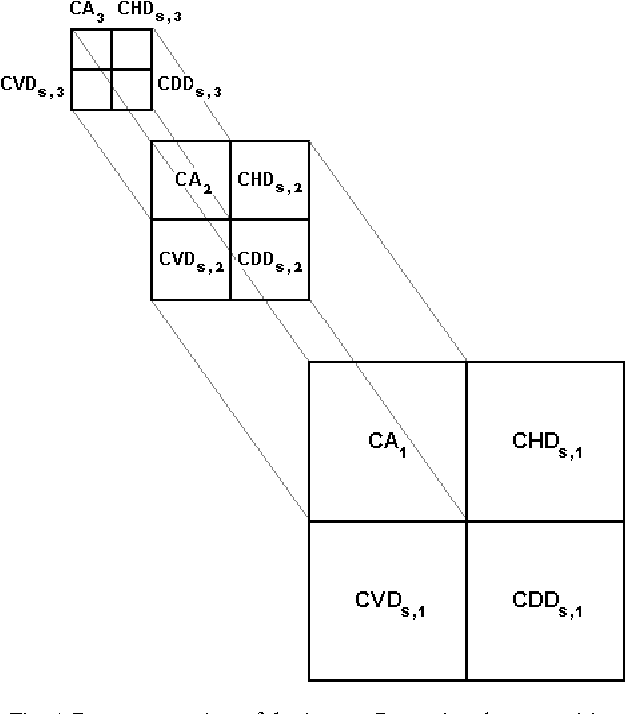
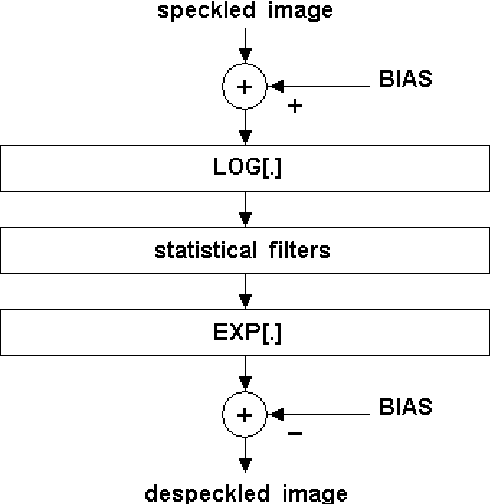
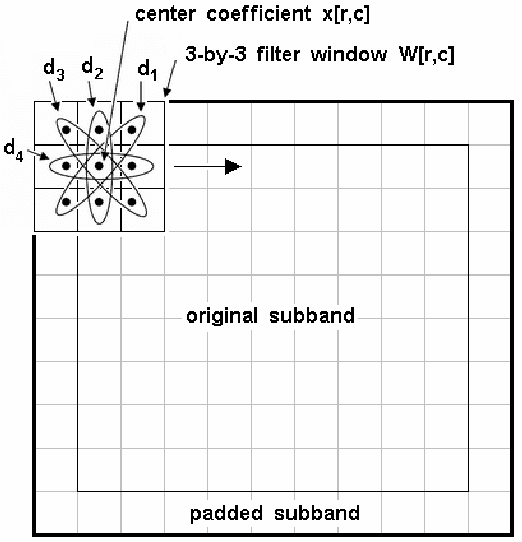
The application of wavelet transforms to Synthetic Aperture Radar (SAR) imagery has improved despeckling performance. To deduce the problem of filtering the multiplicative noise to the case of an additive noise, the wavelet decomposition is performed on the logarithm of the image gray levels. The detail coefficients produced by the bidimensional discrete wavelet transform (DWT-2D) needs to be thresholded to extract out the speckle in highest subbands. An initial threshold value is estimated according to the noise variance. In this paper, an additional fuzzy thresholding approach for automatic determination of the rate threshold level around the traditional wavelet noise thresholding (initial threshold) is applied, and used for the soft or hard-threshold performed on all the high frequency subimages. The filtered logarithmic image is then obtained by reconstruction from the thresholded coefficients. This process is applied a single time, and exclusively to the first level of decomposition. The exponential function of this reconstructed image gives the final filtered image. Experimental results on test images have demonstrated the effectiveness of this method compared to the most of methods in use at the moment.

Denoising based on wavelets and deblurring via self-organizing map for Synthetic Aperture Radar images

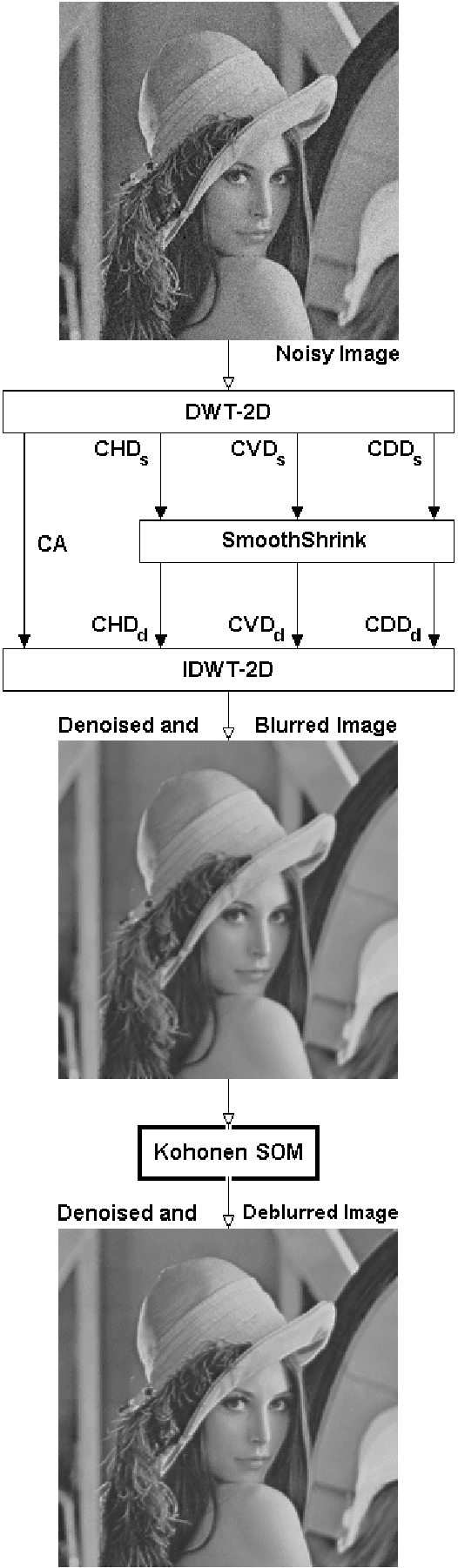
This work deals with unsupervised image deblurring. We present a new deblurring procedure on images provided by low-resolution synthetic aperture radar (SAR) or simply by multimedia in presence of multiplicative (speckle) or additive noise, respectively. The method we propose is defined as a two-step process. First, we use an original technique for noise reduction in wavelet domain. Then, the learning of a Kohonen self-organizing map (SOM) is performed directly on the denoised image to take out it the blur. This technique has been successfully applied to real SAR images, and the simulation results are presented to demonstrate the effectiveness of the proposed algorithms.

Kalman's shrinkage for wavelet-based despeckling of SAR images

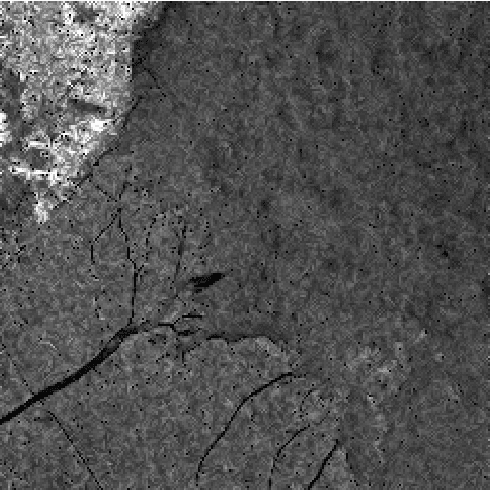
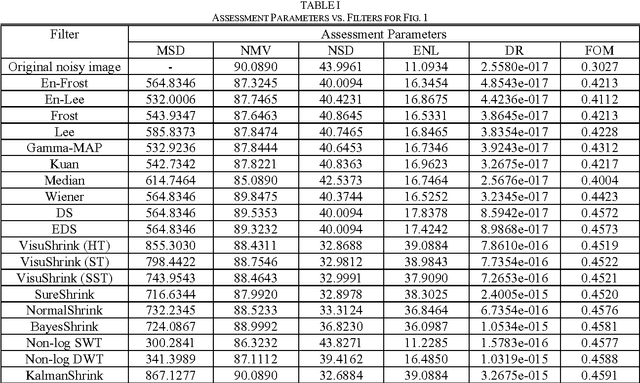
In this paper, a new probability density function (pdf) is proposed to model the statistics of wavelet coefficients, and a simple Kalman's filter is derived from the new pdf using Bayesian estimation theory. Specifically, we decompose the speckled image into wavelet subbands, we apply the Kalman's filter to the high subbands, and reconstruct a despeckled image from the modified detail coefficients. Experimental results demonstrate that our method compares favorably to several other despeckling methods on test synthetic aperture radar (SAR) images.

New wavelet-based superresolution algorithm for speckle reduction in SAR images

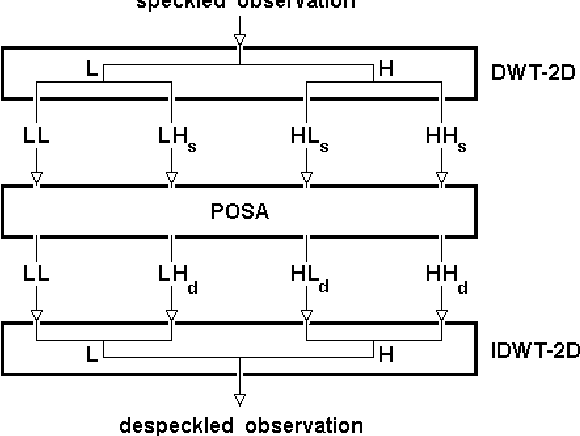
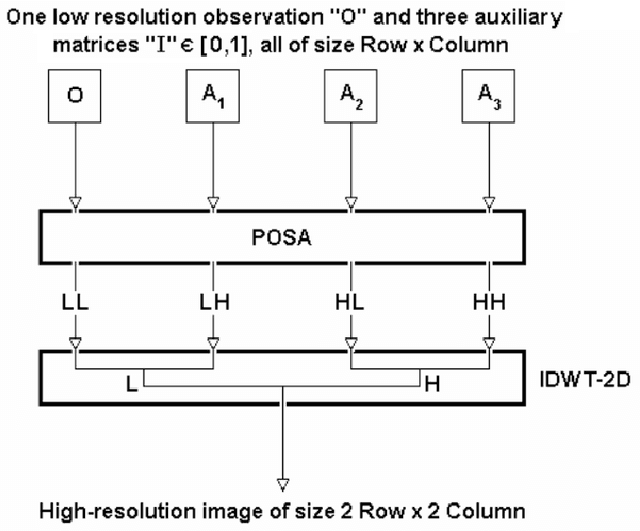
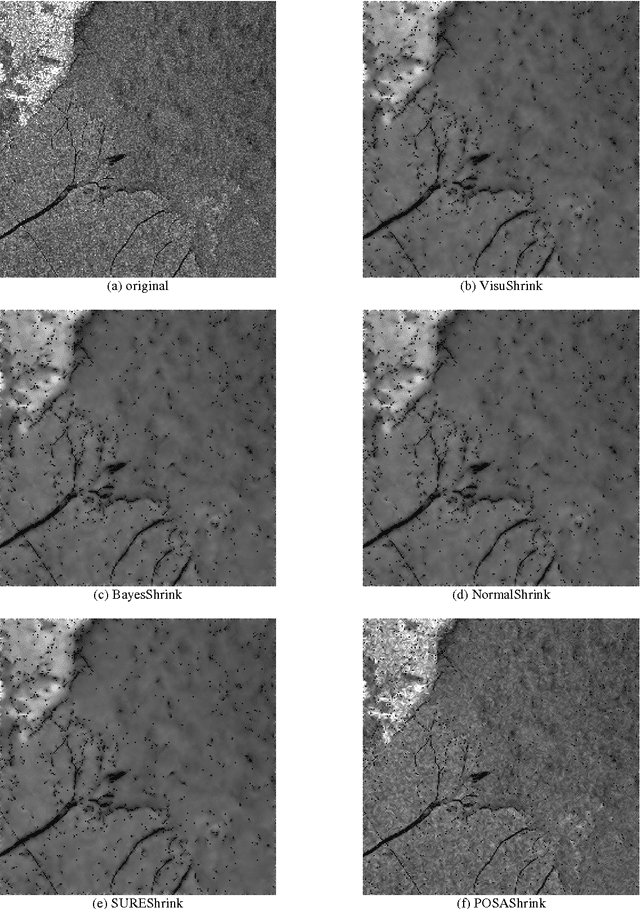
This paper describes a novel projection algorithm, the Projection Onto Span Algorithm (POSA) for wavelet-based superresolution and removing speckle (in wavelet domain) of unknown variance from Synthetic Aperture Radar (SAR) images. Although the POSA is good as a new superresolution algorithm for image enhancement, image metrology and biometric identification, here one will use it like a tool of despeckling, being the first time that an algorithm of super-resolution is used for despeckling of SAR images. Specifically, the speckled SAR image is decomposed into wavelet subbands, POSA is applied to the high subbands, and reconstruct a SAR image from the modified detail coefficients. Experimental results demonstrate that the new method compares favorably to several other despeckling methods on test SAR images.

Union is strength in lossy image compression

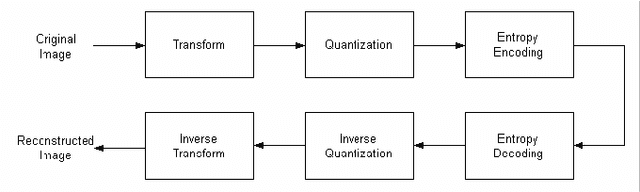
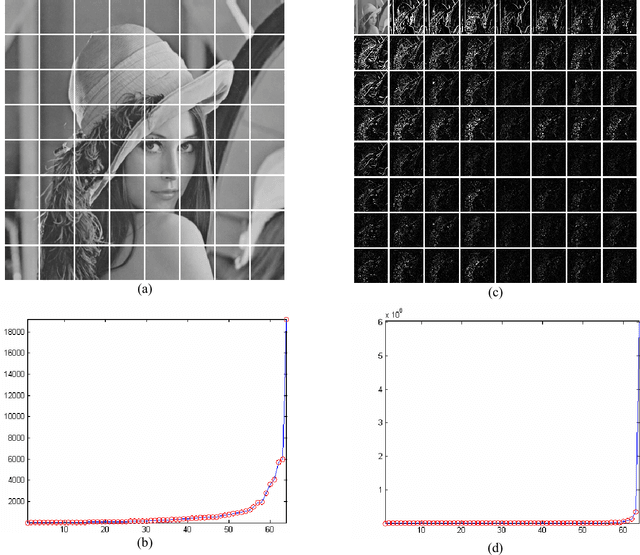
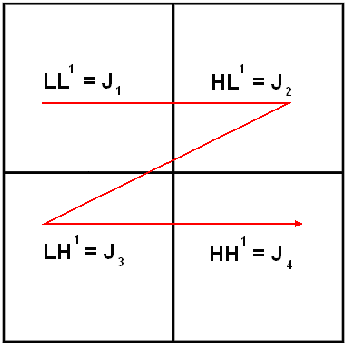
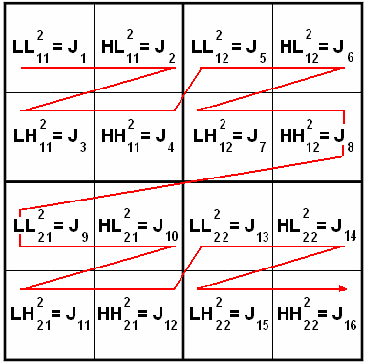
In this work, we present a comparison between different techniques of image compression. First, the image is divided in blocks which are organized according to a certain scan. Later, several compression techniques are applied, combined or alone. Such techniques are: wavelets (Haar's basis), Karhunen-Loeve Transform, etc. Simulations show that the combined versions are the best, with minor Mean Squared Error (MSE), and higher Peak Signal to Noise Ratio (PSNR) and better image quality, even in the presence of noise.

Denoising and compression in wavelet domain via projection onto approximation coefficients

We describe a new filtering approach in the wavelet domain for image denoising and compression, based on the projections of details subbands coefficients (resultants of the splitting procedure, typical in wavelet domain) onto the approximation subband coefficients (much less noisy). The new algorithm is called Projection Onto Approximation Coefficients (POAC). As a result of this approach, only the approximation subband coefficients and three scalars are stored and/or transmitted to the channel. Besides, with the elimination of the details subbands coefficients, we obtain a bigger compression rate. Experimental results demonstrate that our approach compares favorably to more typical methods of denoising and compression in wavelet domain.

New version of Gram-Schmidt Process with inverse for Signal and Image Processing

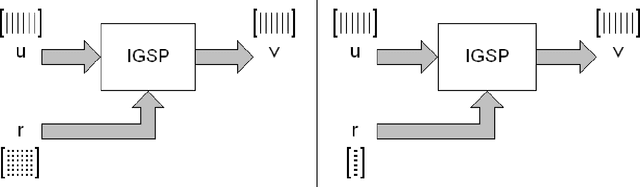
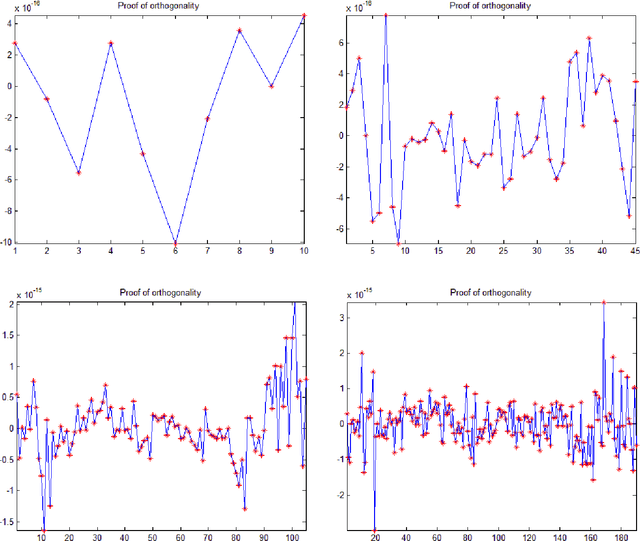
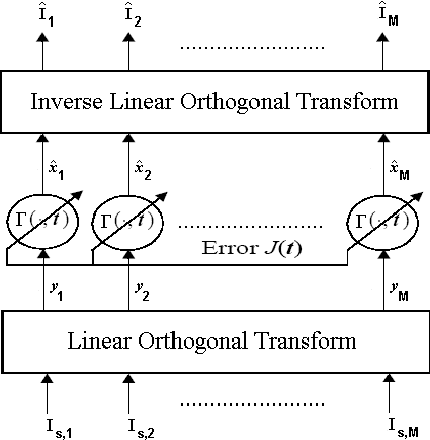
The Gram-Schmidt Process (GSP) is used to convert a non-orthogonal basis (a set of linearly independent vectors, matrices, etc) into an orthonormal basis (a set of orthogonal, unit-length vectors, bi or tri dimensional matrices). The process consists of taking each array and then subtracting the projections in common with the previous arrays. This paper introduces an enhanced version of the Gram-Schmidt Process (EGSP) with inverse, which is useful for Digital Signal and Image Processing, among others applications.