Enhanced Directional Smoothing Algorithm for Edge-Preserving Smoothing of Synthetic-Aperture Radar Images

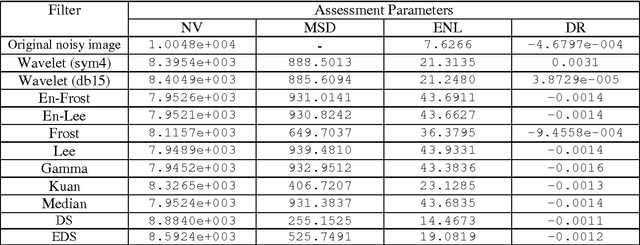
Synthetic aperture radar (SAR) images are subject to prominent speckle noise, which is generally considered a purely multiplicative noise process. In theory, this multiplicative noise is that the ratio of the standard deviation to the signal value, the "coefficient of variation," is theoretically constant at every point in a SAR image. Most of the filters for speckle reduction are based on this property. Such property is irrelevant for the new filter structure, which is based on directional smoothing (DS) theory, the enhanced directional smoothing (EDS) that removes speckle noise from SAR images without blurring edges. We demonstrate the effectiveness of this new filtering method by comparing it to established speckle noise removal techniques on SAR images.

Neural shrinkage for wavelet-based SAR despeckling

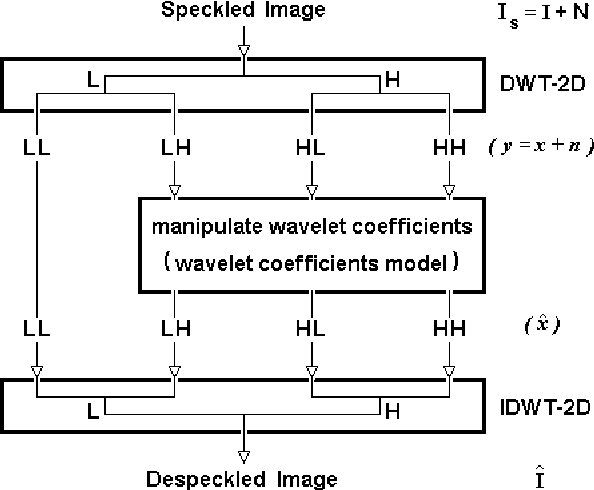
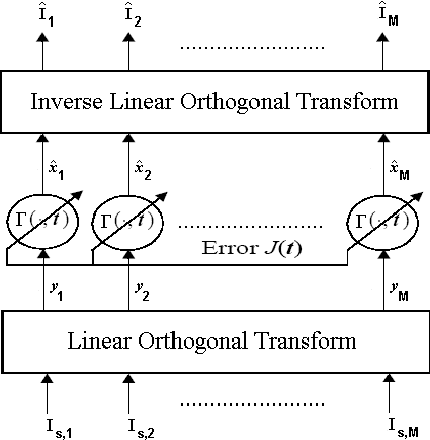
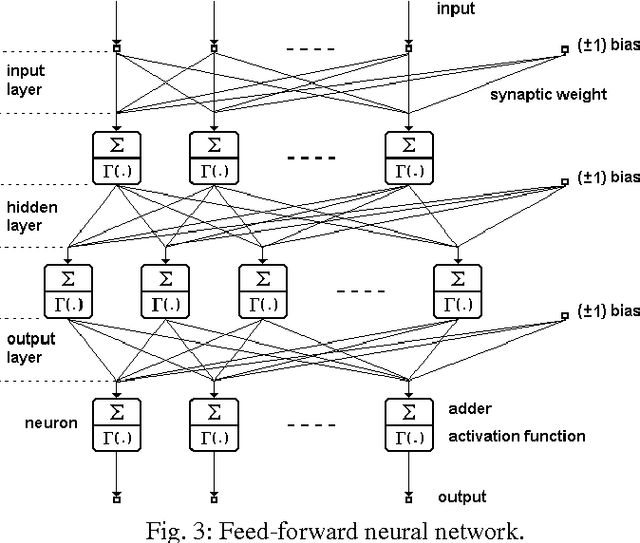
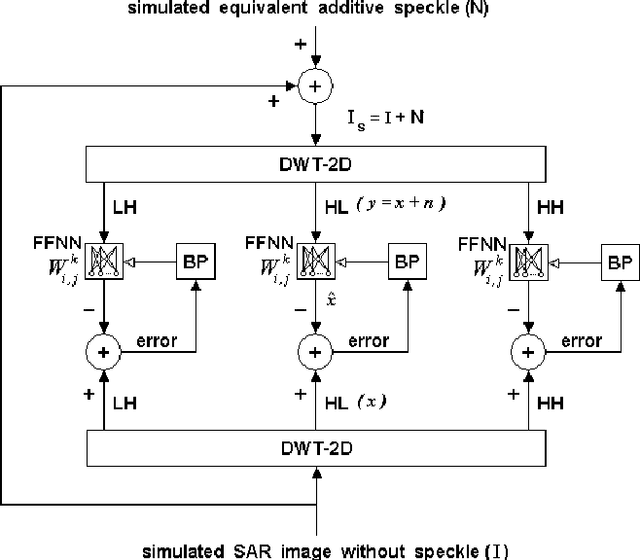
The wavelet shrinkage denoising approach is able to maintain local regularity of a signal while suppressing noise. However, the conventional wavelet shrinkage based methods are not time-scale adaptive to track the local time-scale variation. In this paper, a new type of Neural Shrinkage (NS) is presented with a new class of shrinkage architecture for speckle reduction in Synthetic Aperture Radar (SAR) images. The numerical results indicate that the new method outperforms the standard filters, the standard wavelet shrinkage despeckling method, and previous NS.

Kalman's shrinkage for wavelet-based despeckling of SAR images

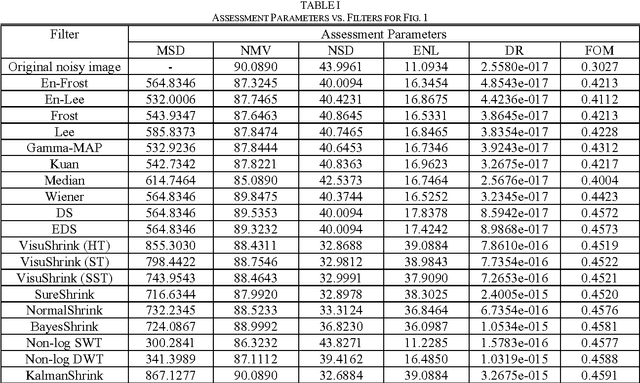
In this paper, a new probability density function (pdf) is proposed to model the statistics of wavelet coefficients, and a simple Kalman's filter is derived from the new pdf using Bayesian estimation theory. Specifically, we decompose the speckled image into wavelet subbands, we apply the Kalman's filter to the high subbands, and reconstruct a despeckled image from the modified detail coefficients. Experimental results demonstrate that our method compares favorably to several other despeckling methods on test synthetic aperture radar (SAR) images.