Envelopes and Waves: Safe Multivehicle Collision Avoidance for Horizontal Non-deterministic Turns

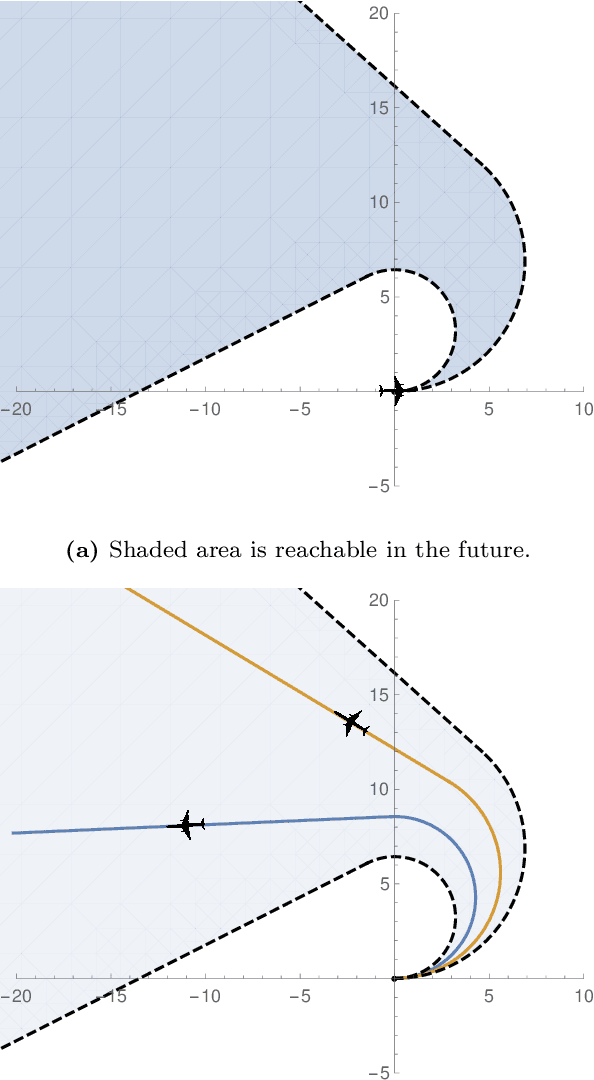
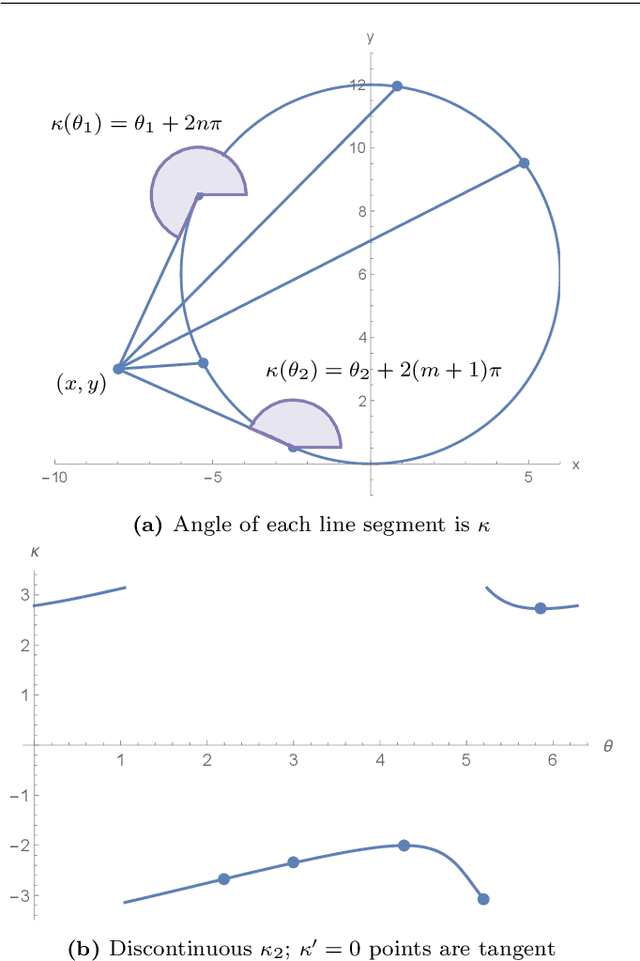
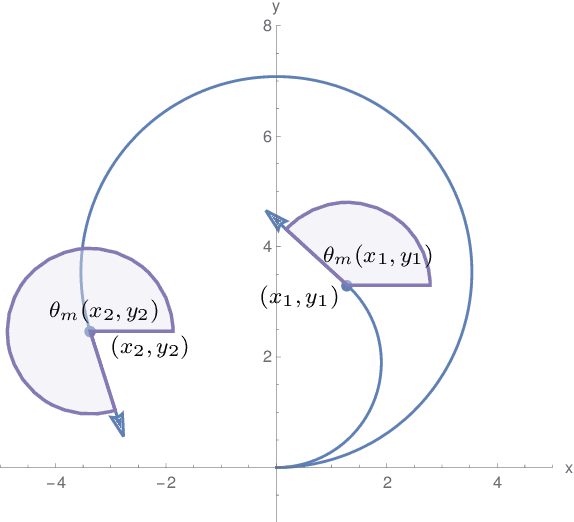
We present an approach to analyzing the safety of asynchronous, independent, non-deterministic, turn-to-bearing horizontal maneuvers for two vehicles. Future turn rates, final bearings, and continuously varying ground speeds throughout the encounter are unknown but restricted to known ranges. We develop a library of formal proofs about turning kinematics, and apply the library to create a formally verified timing computation. Additionally, we create a technique that evaluates future collision possibilities that is based on waves of position possibilities and relies on the timing computation. The result either determines that the encounter will be collision-free, or computes a safe overapproximation for when and where collisions may occur.

Incorrect by Construction: Fine Tuning Neural Networks for Guaranteed Performance on Finite Sets of Examples

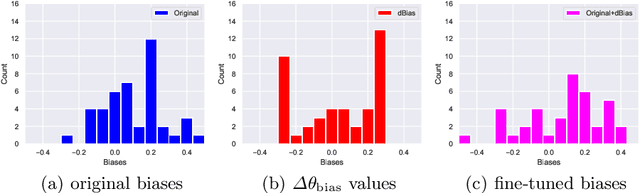
There is great interest in using formal methods to guarantee the reliability of deep neural networks. However, these techniques may also be used to implant carefully selected input-output pairs. We present initial results on a novel technique for using SMT solvers to fine tune the weights of a ReLU neural network to guarantee outcomes on a finite set of particular examples. This procedure can be used to ensure performance on key examples, but it could also be used to insert difficult-to-find incorrect examples that trigger unexpected performance. We demonstrate this approach by fine tuning an MNIST network to incorrectly classify a particular image and discuss the potential for the approach to compromise reliability of freely-shared machine learning models.

Whittemore: An embedded domain specific language for causal programming

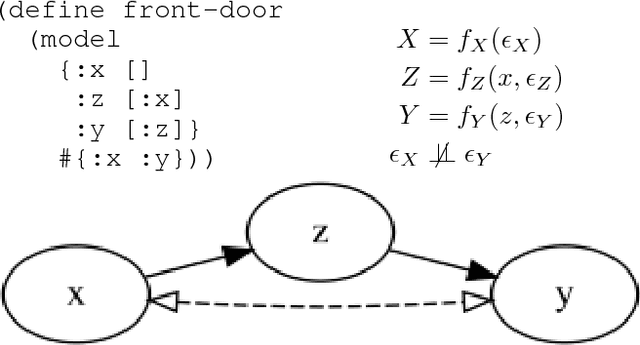
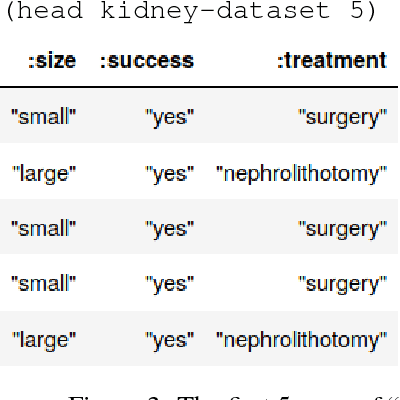
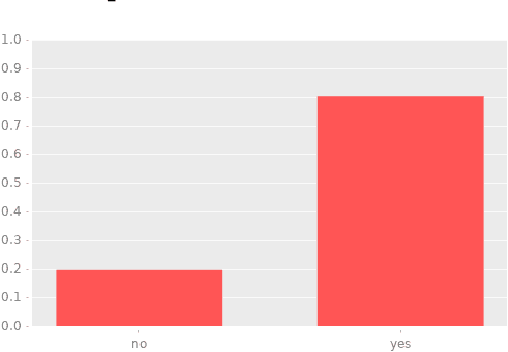
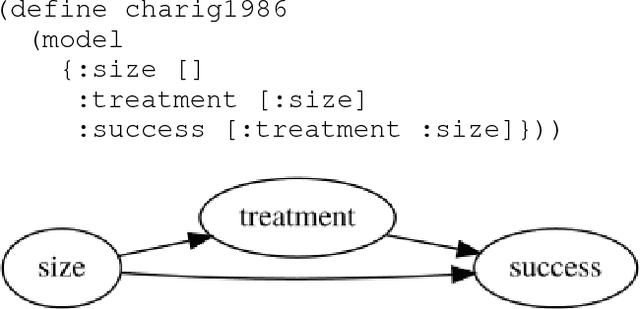
This paper introduces Whittemore, a language for causal programming. Causal programming is based on the theory of structural causal models and consists of two primary operations: identification, which finds formulas that compute causal queries, and estimation, which applies formulas to transform probability distributions to other probability distribution. Causal programming provides abstractions to declare models, queries, and distributions with syntax similar to standard mathematical notation, and conducts rigorous causal inference, without requiring detailed knowledge of the underlying algorithms. Examples of causal inference with real data are provided, along with discussion of the implementation and possibilities for future extension.

Causal programming: inference with structural causal models as finding instances of a relation

This paper proposes a causal inference relation and causal programming as general frameworks for causal inference with structural causal models. A tuple, $\langle M, I, Q, F \rangle$, is an instance of the relation if a formula, $F$, computes a causal query, $Q$, as a function of known population probabilities, $I$, in every model entailed by a set of model assumptions, $M$. Many problems in causal inference can be viewed as the problem of enumerating instances of the relation that satisfy given criteria. This unifies a number of previously studied problems, including causal effect identification, causal discovery and recovery from selection bias. In addition, the relation supports formalizing new problems in causal inference with structural causal models, such as the problem of research design. Causal programming is proposed as a further generalization of causal inference as the problem of finding optimal instances of the relation, with respect to a cost function.

A causation coefficient and taxonomy of correlation/causation relationships

This paper introduces a causation coefficient which is defined in terms of probabilistic causal models. This coefficient is suggested as the natural causal analogue of the Pearson correlation coefficient and permits comparing causation and correlation to each other in a simple, yet rigorous manner. Together, these coefficients provide a natural way to classify the possible correlation/causation relationships that can occur in practice and examples of each relationship are provided. In addition, the typical relationship between correlation and causation is analyzed to provide insight into why correlation and causation are often conflated. Finally, example calculations of the causation coefficient are shown on a real data set.

Evolving Shepherding Behavior with Genetic Programming Algorithms

We apply genetic programming techniques to the `shepherding' problem, in which a group of one type of animal (sheep dogs) attempts to control the movements of a second group of animals (sheep) obeying flocking behavior. Our genetic programming algorithm evolves an expression tree that governs the movements of each dog. The operands of the tree are hand-selected features of the simulation environment that may allow the dogs to herd the sheep effectively. The algorithm uses tournament-style selection, crossover reproduction, and a point mutation. We find that the evolved solutions generalize well and outperform a (naive) human-designed algorithm.

The Computational Power of Dynamic Bayesian Networks

This paper considers the computational power of constant size, dynamic Bayesian networks. Although discrete dynamic Bayesian networks are no more powerful than hidden Markov models, dynamic Bayesian networks with continuous random variables and discrete children of continuous parents are capable of performing Turing-complete computation. With modified versions of existing algorithms for belief propagation, such a simulation can be carried out in real time. This result suggests that dynamic Bayesian networks may be more powerful than previously considered. Relationships to causal models and recurrent neural networks are also discussed.