Social learning with complex contagion

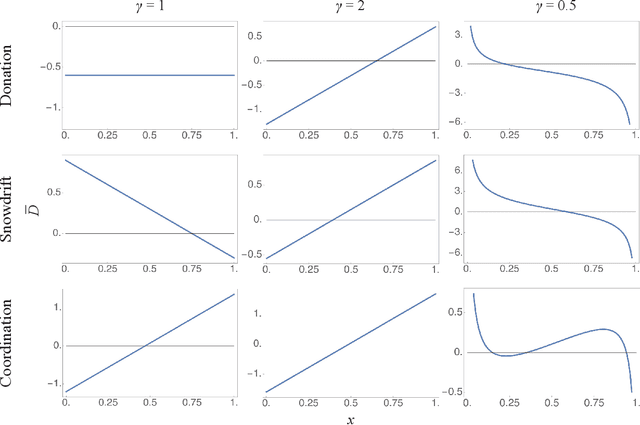
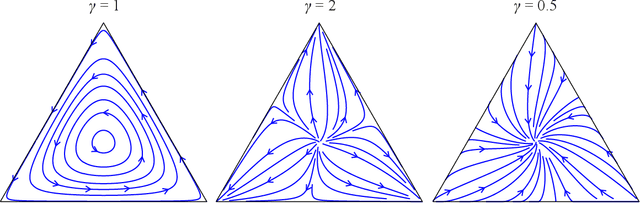
We introduce a mathematical model that combines the concepts of complex contagion with payoff-biased imitation, to describe how social behaviors spread through a population. Traditional models of social learning by imitation are based on simple contagion -- where an individual may imitate a more successful neighbor following a single interaction. Our framework generalizes this process to incorporate complex contagion, which requires multiple exposures before an individual considers adopting a different behavior. We formulate this as a discrete time and state stochastic process in a finite population, and we derive its continuum limit as an ordinary differential equation that generalizes the replicator equation, the most widely used dynamical model in evolutionary game theory. When applied to linear frequency-dependent games, our social learning with complex contagion produces qualitatively different outcomes than traditional imitation dynamics: it can shift the Prisoner's Dilemma from a unique all-defector equilibrium to either a stable mixture of cooperators and defectors in the population, or a bistable system; it changes the Snowdrift game from a single to a bistable equilibrium; and it can alter the Coordination game from bistability at the boundaries to two internal equilibria. The long-term outcome depends on the balance between the complexity of the contagion process and the strength of selection that biases imitation towards more successful types. Our analysis intercalates the fields of evolutionary game theory with complex contagions, and it provides a synthetic framework that describes more realistic forms of behavioral change in social systems.

Evolutionary forces in language change

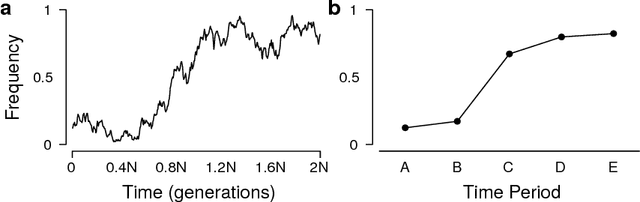
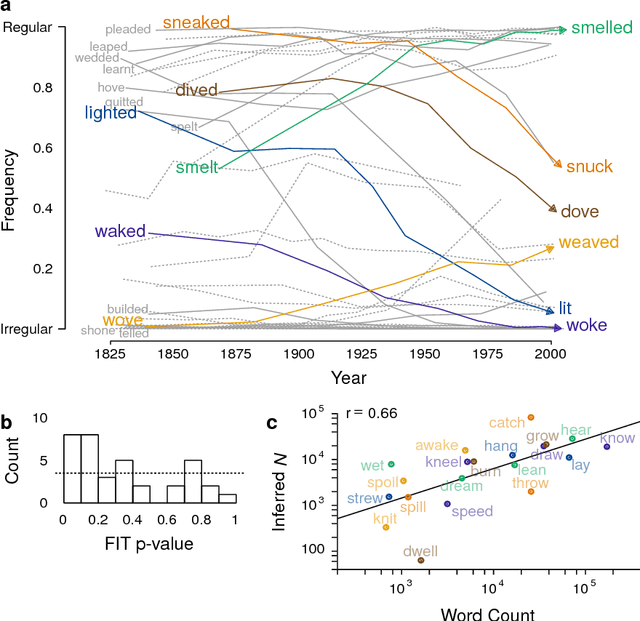
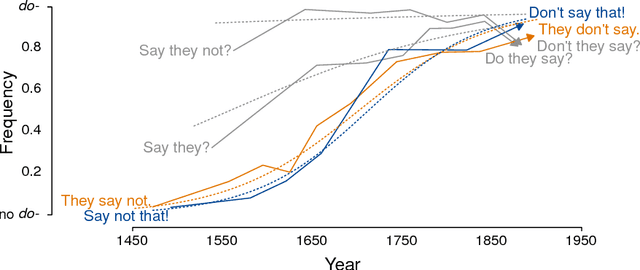
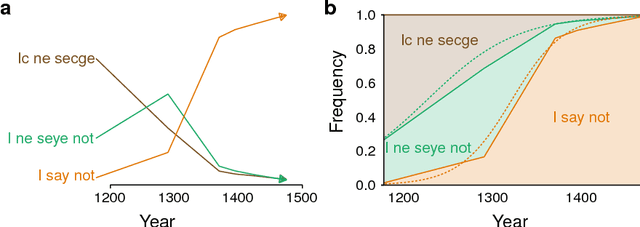
Languages and genes are both transmitted from generation to generation, with opportunity for differential reproduction and survivorship of forms. Here we apply a rigorous inference framework, drawn from population genetics, to distinguish between two broad mechanisms of language change: drift and selection. Drift is change that results from stochasticity in transmission and it may occur in the absence of any intrinsic difference between linguistic forms; whereas selection is truly an evolutionary force arising from intrinsic differences -- for example, when one form is preferred by members of the population. Using large corpora of parsed texts spanning the 12th century to the 21st century, we analyze three examples of grammatical changes in English: the regularization of past-tense verbs, the rise of the periphrastic `do', and syntactic variation in verbal negation. We show that we can reject stochastic drift in favor of a selective force driving some of these language changes, but not others. The strength of drift depends on a word's frequency, and so drift provides an alternative explanation for why some words are more prone to change than others. Our results suggest an important role for stochasticity in language change, and they provide a null model against which selective theories of language evolution must be compared.