Social learning with complex contagion
Paper and Code
Jun 21, 2024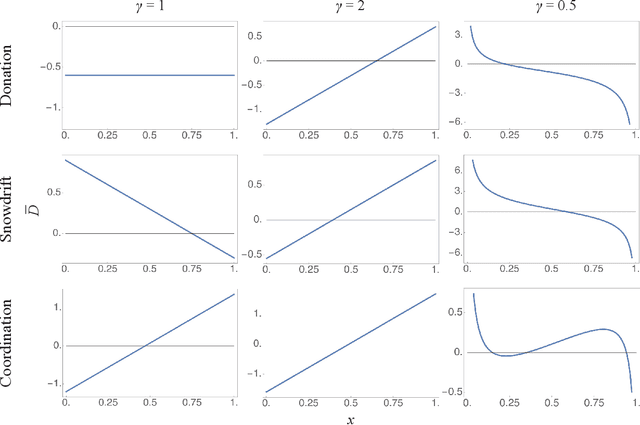


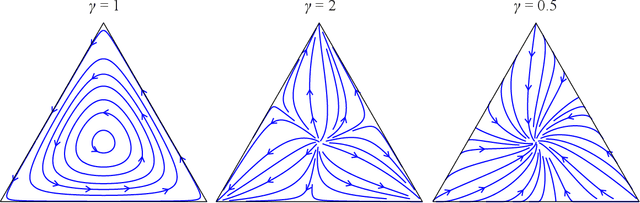
We introduce a mathematical model that combines the concepts of complex contagion with payoff-biased imitation, to describe how social behaviors spread through a population. Traditional models of social learning by imitation are based on simple contagion -- where an individual may imitate a more successful neighbor following a single interaction. Our framework generalizes this process to incorporate complex contagion, which requires multiple exposures before an individual considers adopting a different behavior. We formulate this as a discrete time and state stochastic process in a finite population, and we derive its continuum limit as an ordinary differential equation that generalizes the replicator equation, the most widely used dynamical model in evolutionary game theory. When applied to linear frequency-dependent games, our social learning with complex contagion produces qualitatively different outcomes than traditional imitation dynamics: it can shift the Prisoner's Dilemma from a unique all-defector equilibrium to either a stable mixture of cooperators and defectors in the population, or a bistable system; it changes the Snowdrift game from a single to a bistable equilibrium; and it can alter the Coordination game from bistability at the boundaries to two internal equilibria. The long-term outcome depends on the balance between the complexity of the contagion process and the strength of selection that biases imitation towards more successful types. Our analysis intercalates the fields of evolutionary game theory with complex contagions, and it provides a synthetic framework that describes more realistic forms of behavioral change in social systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge