Blockwise SURE Shrinkage for Non-Local Means

In this letter, we investigate the shrinkage problem for the non-local means (NLM) image denoising. In particular, we derive the closed-form of the optimal blockwise shrinkage for NLM that minimizes the Stein's unbiased risk estimator (SURE). We also propose a constant complexity algorithm allowing fast blockwise shrinkage. Simulation results show that the proposed blockwise shrinkage method improves NLM performance in attaining higher peak signal noise ratio (PSNR) and structural similarity index (SSIM), and makes NLM more robust against parameter changes. Similar ideas can be applicable to other patchwise image denoising techniques.

Probabilistic Non-Local Means

In this paper, we propose a so-called probabilistic non-local means (PNLM) method for image denoising. Our main contributions are: 1) we point out defects of the weight function used in the classic NLM; 2) we successfully derive all theoretical statistics of patch-wise differences for Gaussian noise; and 3) we employ this prior information and formulate the probabilistic weights truly reflecting the similarity between two noisy patches. The probabilistic nature of the new weight function also provides a theoretical basis to choose thresholds rejecting dissimilar patches for fast computations. Our simulation results indicate the PNLM outperforms the classic NLM and many NLM recent variants in terms of peak signal noise ratio (PSNR) and structural similarity (SSIM) index. Encouraging improvements are also found when we replace the NLM weights with the probabilistic weights in tested NLM variants.

James-Stein Type Center Pixel Weights for Non-Local Means Image Denoising

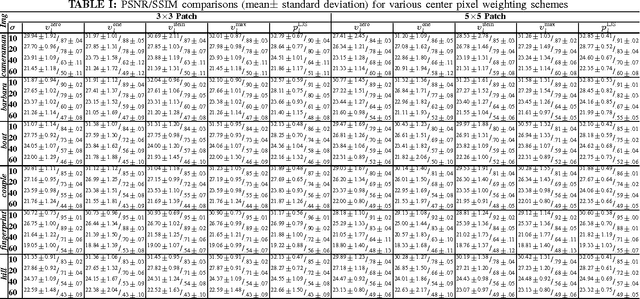
Non-Local Means (NLM) and variants have been proven to be effective and robust in many image denoising tasks. In this letter, we study the parameter selection problem of center pixel weights (CPW) in NLM. Our key contributions are: 1) we give a novel formulation of the CPW problem from the statistical shrinkage perspective; 2) we introduce the James-Stein type CPWs for NLM; and 3) we propose a new adaptive CPW that is locally tuned for each image pixel. Our experimental results showed that compared to existing CPW solutions, the new proposed CPWs are more robust and effective under various noise levels. In particular, the NLM with the James-Stein type CPWs attain higher means with smaller variances in terms of the peak signal and noise ratio, implying they improve the NLM robustness and make it less sensitive to parameter selection.

A New Randomness Evaluation Method with Applications to Image Shuffling and Encryption

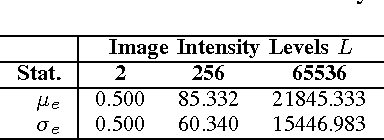
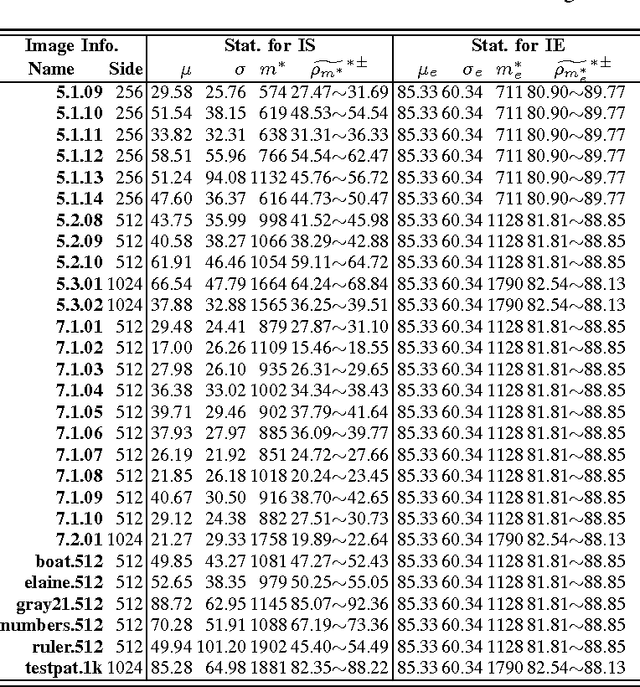
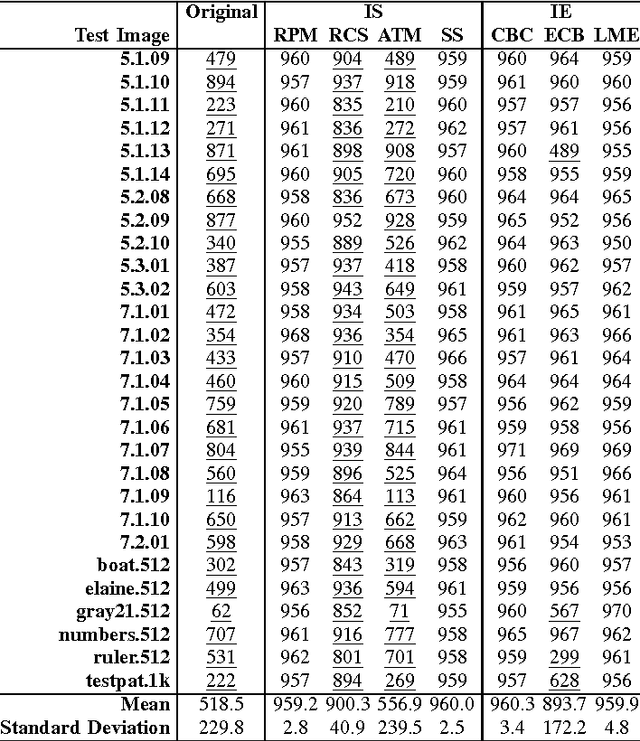
This letter discusses the problem of testing the degree of randomness within an image, particularly for a shuffled or encrypted image. Its key contributions are: 1) a mathematical model of perfectly shuffled images; 2) the derivation of the theoretical distribution of pixel differences; 3) a new $Z$-test based approach to differentiate whether or not a test image is perfectly shuffled; and 4) a randomized algorithm to unbiasedly evaluate the degree of randomness within a given image. Simulation results show that the proposed method is robust and effective in evaluating the degree of randomness within an image, and may often be more suitable for image applications than commonly used testing schemes designed for binary data like NIST 800-22. The developed method may be also useful as a first step in determining whether or not a shuffling or encryption scheme is suitable for a particular cryptographic application.