James-Stein Type Center Pixel Weights for Non-Local Means Image Denoising
Paper and Code
Nov 07, 2012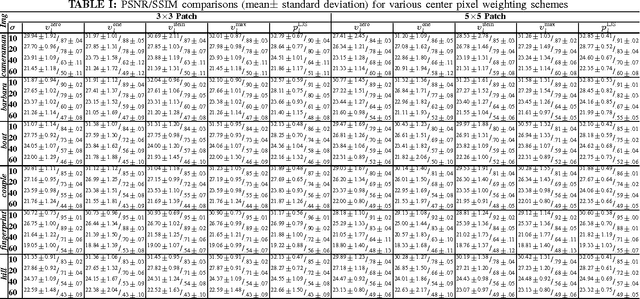
Non-Local Means (NLM) and variants have been proven to be effective and robust in many image denoising tasks. In this letter, we study the parameter selection problem of center pixel weights (CPW) in NLM. Our key contributions are: 1) we give a novel formulation of the CPW problem from the statistical shrinkage perspective; 2) we introduce the James-Stein type CPWs for NLM; and 3) we propose a new adaptive CPW that is locally tuned for each image pixel. Our experimental results showed that compared to existing CPW solutions, the new proposed CPWs are more robust and effective under various noise levels. In particular, the NLM with the James-Stein type CPWs attain higher means with smaller variances in terms of the peak signal and noise ratio, implying they improve the NLM robustness and make it less sensitive to parameter selection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge