Joseph A. Fernandez
Zero-Aliasing Correlation Filters for Object Recognition
Nov 19, 2014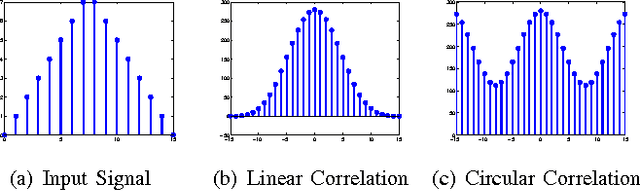

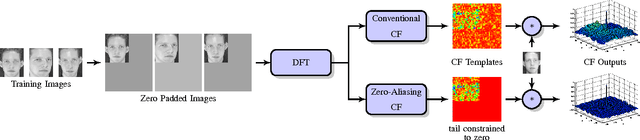
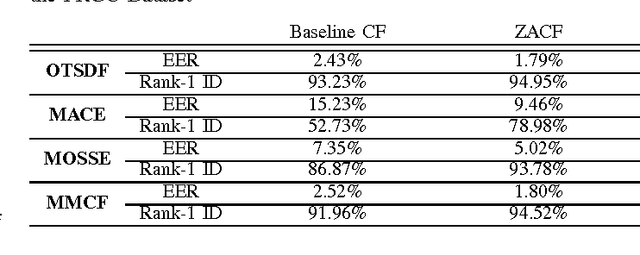
Abstract:Correlation filters (CFs) are a class of classifiers that are attractive for object localization and tracking applications. Traditionally, CFs have been designed in the frequency domain using the discrete Fourier transform (DFT), where correlation is efficiently implemented. However, existing CF designs do not account for the fact that the multiplication of two DFTs in the frequency domain corresponds to a circular correlation in the time/spatial domain. Because this was previously unaccounted for, prior CF designs are not truly optimal, as their optimization criteria do not accurately quantify their optimization intention. In this paper, we introduce new zero-aliasing constraints that completely eliminate this aliasing problem by ensuring that the optimization criterion for a given CF corresponds to a linear correlation rather than a circular correlation. This means that previous CF designs can be significantly improved by this reformulation. We demonstrate the benefits of this new CF design approach with several important CFs. We present experimental results on diverse data sets and present solutions to the computational challenges associated with computing these CFs. Code for the CFs described in this paper and their respective zero-aliasing versions is available at http://vishnu.boddeti.net/projects/correlation-filters.html
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge