Sharp Bounds of the Causal Effect Under MNAR Confounding

We report bounds for any contrast between the probabilities of the counterfactual outcome under exposure and non-exposure when the confounders are missing not at random. We assume that the missingness mechanism is outcome-independent, and prove that our bounds are arbitrarily sharp, i.e., practically attainable or logically possible.

Simple yet Sharp Sensitivity Analysis for Any Contrast Under Unmeasured Confounding

We extend our previous work on sensitivity analysis for the risk ratio and difference contrasts under unmeasured confounding to any contrast. We prove that the bounds produced are still arbitrarily sharp, i.e. practically attainable. We illustrate the usability of the bounds with real data.

Deep Learning With DAGs

Social science theories often postulate causal relationships among a set of variables or events. Although directed acyclic graphs (DAGs) are increasingly used to represent these theories, their full potential has not yet been realized in practice. As non-parametric causal models, DAGs require no assumptions about the functional form of the hypothesized relationships. Nevertheless, to simplify the task of empirical evaluation, researchers tend to invoke such assumptions anyway, even though they are typically arbitrary and do not reflect any theoretical content or prior knowledge. Moreover, functional form assumptions can engender bias, whenever they fail to accurately capture the complexity of the causal system under investigation. In this article, we introduce causal-graphical normalizing flows (cGNFs), a novel approach to causal inference that leverages deep neural networks to empirically evaluate theories represented as DAGs. Unlike conventional approaches, cGNFs model the full joint distribution of the data according to a DAG supplied by the analyst, without relying on stringent assumptions about functional form. In this way, the method allows for flexible, semi-parametric estimation of any causal estimand that can be identified from the DAG, including total effects, conditional effects, direct and indirect effects, and path-specific effects. We illustrate the method with a reanalysis of Blau and Duncan's (1967) model of status attainment and Zhou's (2019) model of conditional versus controlled mobility. To facilitate adoption, we provide open-source software together with a series of online tutorials for implementing cGNFs. The article concludes with a discussion of current limitations and directions for future development.

On the Probability of Immunity

This work is devoted to the study of the probability of immunity, i.e. the effect occurs whether exposed or not. We derive necessary and sufficient conditions for non-immunity and $\epsilon$-bounded immunity, i.e. the probability of immunity is zero and $\epsilon$-bounded, respectively. The former allows us to estimate the probability of benefit (i.e., the effect occurs if and only if exposed) from a randomized controlled trial, and the latter allows us to produce bounds of the probability of benefit that are tighter than the existing ones. We also introduce the concept of indirect immunity (i.e., through a mediator) and repeat our previous analysis for it. Finally, we propose a method for sensitivity analysis of the probability of immunity under unmeasured confounding.

Bounding the Probabilities of Benefit and Harm Through Sensitivity Parameters and Proxies

We present two methods for bounding the probabilities of benefit and harm under unmeasured confounding. The first method computes the (upper or lower) bound of either probability as a function of the observed data distribution and two intuitive sensitivity parameters which, then, can be presented to the analyst as a 2-D plot to assist her in decision making. The second method assumes the existence of a measured nondifferential proxy (i.e., direct effect) of the unmeasured confounder. Using this proxy, tighter bounds than the existing ones can be derived from just the observed data distribution.

$ρ$-GNF : A Novel Sensitivity Analysis Approach Under Unobserved Confounders

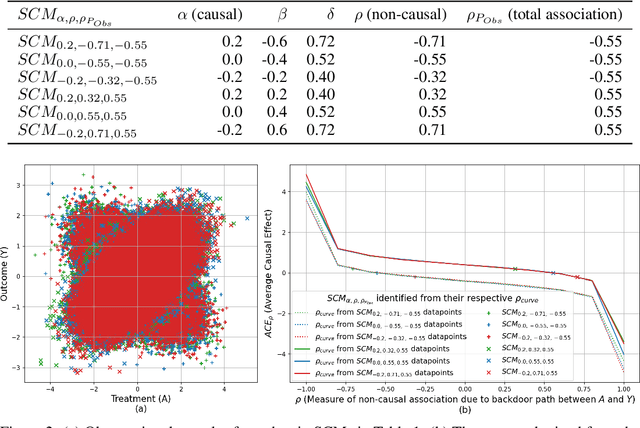
We propose a new sensitivity analysis model that combines copulas and normalizing flows for causal inference under unobserved confounding. We refer to the new model as $\rho$-GNF ($\rho$-Graphical Normalizing Flow), where $\rho{\in}[-1,+1]$ is a bounded sensitivity parameter representing the backdoor non-causal association due to unobserved confounding modeled using the most well studied and widely popular Gaussian copula. Specifically, $\rho$-GNF enables us to estimate and analyse the frontdoor causal effect or average causal effect (ACE) as a function of $\rho$. We call this the $\rho_{curve}$. The $\rho_{curve}$ enables us to specify the confounding strength required to nullify the ACE. We call this the $\rho_{value}$. Further, the $\rho_{curve}$ also enables us to provide bounds for the ACE given an interval of $\rho$ values. We illustrate the benefits of $\rho$-GNF with experiments on simulated and real-world data in terms of our empirical ACE bounds being narrower than other popular ACE bounds.

Counterfactual Analysis of the Impact of the IMF Program on Child Poverty in the Global-South Region using Causal-Graphical Normalizing Flows

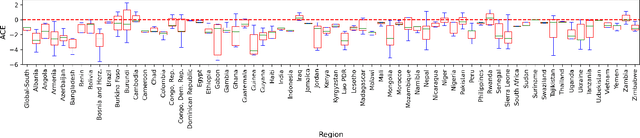
This work demonstrates the application of a particular branch of causal inference and deep learning models: \emph{causal-Graphical Normalizing Flows (c-GNFs)}. In a recent contribution, scholars showed that normalizing flows carry certain properties, making them particularly suitable for causal and counterfactual analysis. However, c-GNFs have only been tested in a simulated data setting and no contribution to date have evaluated the application of c-GNFs on large-scale real-world data. Focusing on the \emph{AI for social good}, our study provides a counterfactual analysis of the impact of the International Monetary Fund (IMF) program on child poverty using c-GNFs. The analysis relies on a large-scale real-world observational data: 1,941,734 children under the age of 18, cared for by 567,344 families residing in the 67 countries from the Global-South. While the primary objective of the IMF is to support governments in achieving economic stability, our results find that an IMF program reduces child poverty as a positive side-effect by about 1.2$\pm$0.24 degree (`0' equals no poverty and `7' is maximum poverty). Thus, our article shows how c-GNFs further the use of deep learning and causal inference in AI for social good. It shows how learning algorithms can be used for addressing the untapped potential for a significant social impact through counterfactual inference at population level (ACE), sub-population level (CACE), and individual level (ICE). In contrast to most works that model ACE or CACE but not ICE, c-GNFs enable personalization using \emph{`The First Law of Causal Inference'}.

Simple yet Sharp Sensitivity Analysis for Unmeasured Confounding

We present a method for assessing the sensitivity of the true causal effect to unmeasured confounding. The method requires the analyst to specify two intuitive parameters. Otherwise, the method is assumption-free. The method returns an interval that contains the true causal effect. Moreover, the bounds of the interval are sharp, i.e. attainable. We show experimentally that our bounds can be sharper than those obtained by the method of Ding and VanderWeele (2016). Finally, we extend our method to bound the natural direct and indirect effects when there are measured mediators and unmeasured exposure-outcome confounding.

On the Non-Monotonicity of a Non-Differentially Mismeasured Binary Confounder

Suppose that we are interested in the average causal effect of a binary treatment on an outcome when this relationship is confounded by a binary confounder. Suppose that the confounder is unobserved but a non-differential binary proxy of it is observed. We identify conditions under which adjusting for the proxy comes closer to the incomputable true average causal effect than not adjusting at all. Unlike other works, we do not assume that the average causal effect of the confounder on the outcome is in the same direction among treated and untreated.

On the Monotonicity of a Nondifferentially Mismeasured Binary Confounder

Suppose that we are interested in the average causal effect of a binary treatment on an outcome when this relationship is confounded by a binary confounder. Suppose that the confounder is unobserved but a nondifferential proxy of it is observed. We show that, under certain monotonicity assumption that is empirically verifiable, adjusting for the proxy produces a measure of the effect that is between the unadjusted and the true measures.