José Antonio Lozano
An efficient K-means algorithm for Massive Data
May 10, 2016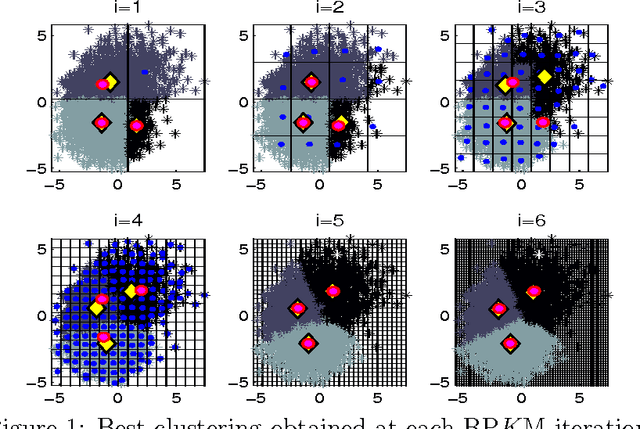

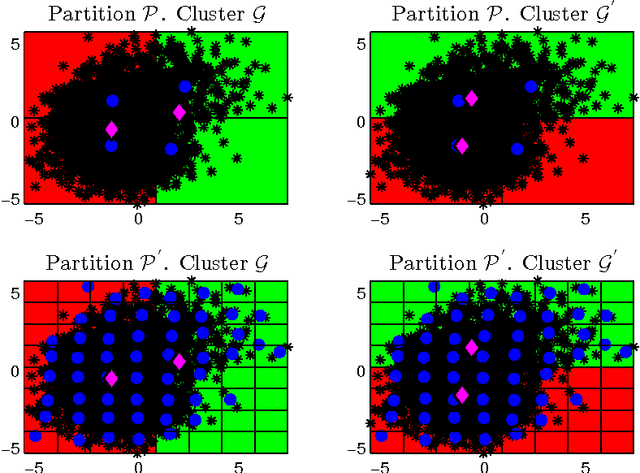
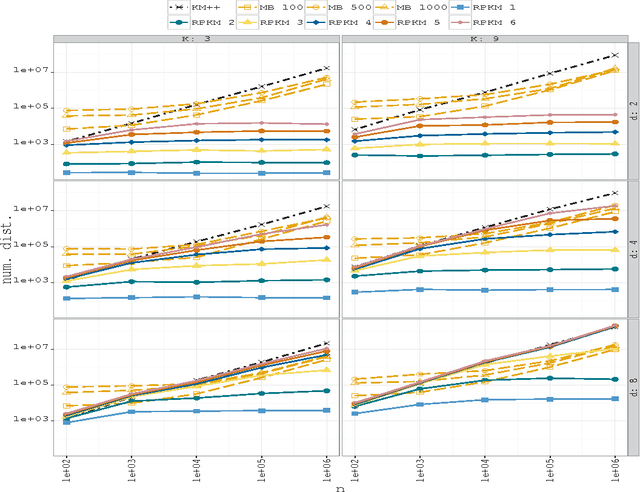
Abstract:Due to the progressive growth of the amount of data available in a wide variety of scientific fields, it has become more difficult to ma- nipulate and analyze such information. Even though datasets have grown in size, the K-means algorithm remains as one of the most popular clustering methods, in spite of its dependency on the initial settings and high computational cost, especially in terms of distance computations. In this work, we propose an efficient approximation to the K-means problem intended for massive data. Our approach recursively partitions the entire dataset into a small number of sub- sets, each of which is characterized by its representative (center of mass) and weight (cardinality), afterwards a weighted version of the K-means algorithm is applied over such local representation, which can drastically reduce the number of distances computed. In addition to some theoretical properties, experimental results indicate that our method outperforms well-known approaches, such as the K-means++ and the minibatch K-means, in terms of the relation between number of distance computations and the quality of the approximation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge