Testing for latent structure via the Wilcoxon--Wigner random matrix of normalized rank statistics

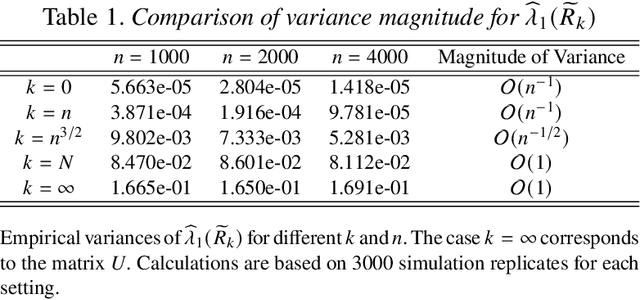
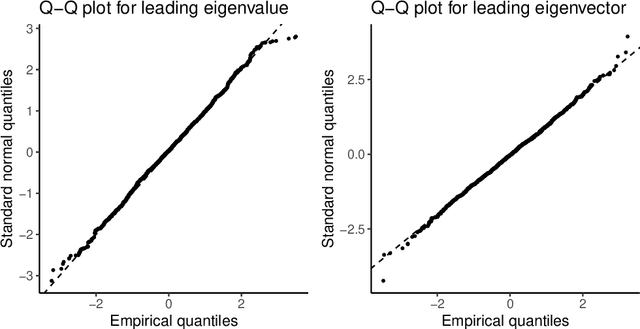
This paper considers the problem of testing for latent structure in large symmetric data matrices. The goal here is to develop statistically principled methodology that is flexible in its applicability, computationally efficient, and insensitive to extreme data variation, thereby overcoming limitations facing existing approaches. To do so, we introduce and systematically study certain symmetric matrices, called Wilcoxon--Wigner random matrices, whose entries are normalized rank statistics derived from an underlying independent and identically distributed sample of absolutely continuous random variables. These matrices naturally arise as the matricization of one-sample problems in statistics and conceptually lie at the interface of nonparametrics, multivariate analysis, and data reduction. Among our results, we establish that the leading eigenvalue and corresponding eigenvector of Wilcoxon--Wigner random matrices admit asymptotically Gaussian fluctuations with explicit centering and scaling terms. These asymptotic results enable rigorous parameter-free and distribution-free spectral methodology for addressing two hypothesis testing problems, namely community detection and principal submatrix detection. Numerical examples illustrate the performance of the proposed approach. Throughout, our findings are juxtaposed with existing results based on the spectral properties of independent entry symmetric random matrices in signal-plus-noise data settings.

Robust spectral clustering with rank statistics

This paper analyzes the statistical performance of a robust spectral clustering method for latent structure recovery in noisy data matrices. We consider eigenvector-based clustering applied to a matrix of nonparametric rank statistics that is derived entrywise from the raw, original data matrix. This approach is robust in the sense that, unlike traditional spectral clustering procedures, it can provably recover population-level latent block structure even when the observed data matrix includes heavy-tailed entries and has a heterogeneous variance profile. Our main theoretical contributions are threefold and hold under flexible data generating conditions. First, we establish that robust spectral clustering with rank statistics can consistently recover latent block structure, viewed as communities of nodes in a graph, in the sense that unobserved community memberships for all but a vanishing fraction of nodes are correctly recovered with high probability when the data matrix is large. Second, we refine the former result and further establish that, under certain conditions, the community membership of any individual, specified node of interest can be asymptotically exactly recovered with probability tending to one in the large-data limit. Third, we establish asymptotic normality results associated with the truncated eigenstructure of matrices whose entries are rank statistics, made possible by synthesizing contemporary entrywise matrix perturbation analysis with the classical nonparametric theory of so-called simple linear rank statistics. Collectively, these results demonstrate the statistical utility of rank-based data transformations when paired with spectral techniques for dimensionality reduction. Additionally, for a dataset of human connectomes, our approach yields parsimonious dimensionality reduction and improved recovery of ground-truth neuroanatomical cluster structure.