Jong-Hoon Ahn
Data-Driven Continuum Dynamics via Transport-Teleport Duality
May 27, 2020
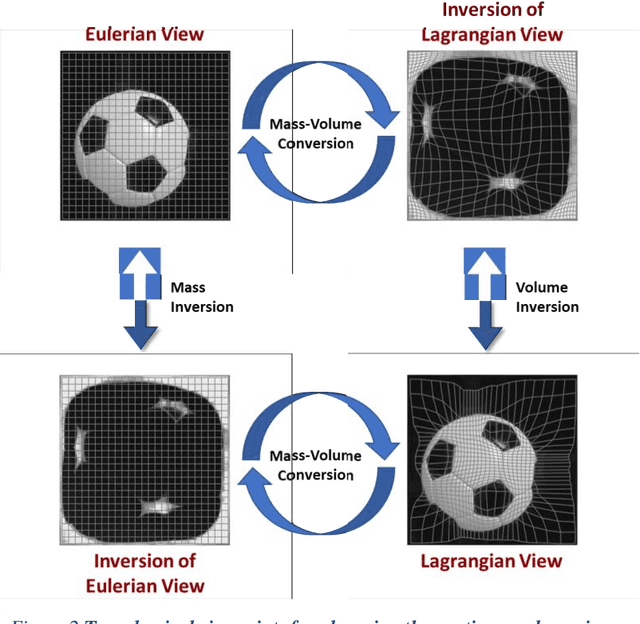
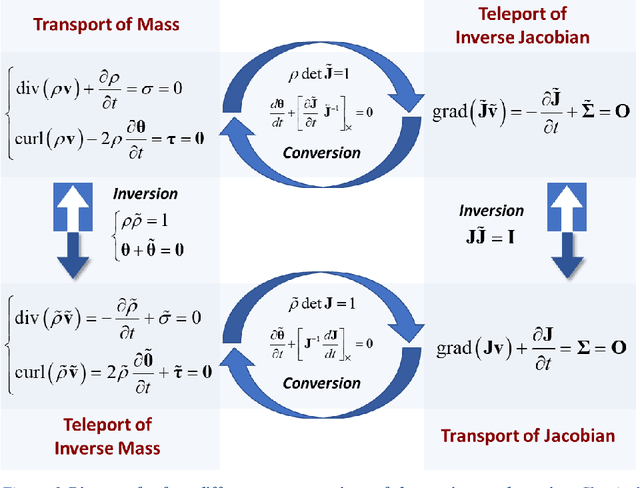
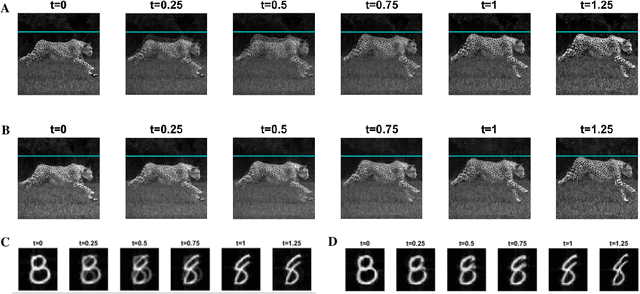
Abstract:In recent years, machine learning methods have been widely used to study physical systems that are challenging to solve with governing equations. However, most learning architectures do not inherently incorporate conservation laws in the form of continuity equations, and they require dense data to learn the continuum dynamics of conserved quantities. In this study, we propose a mathematical framework for machine learning of transport phenomena. Through the derived involution, the continuity equation becomes a pointwise operation for disappearance and reappearance of a quantity with zero velocity. By modeling the process with sparse observations, we can determine and predict the dynamics of a physical system. The approach does not require the explicit use of governing equations and only depends on observation data.
Lipschitz Learning for Signal Recovery
Oct 04, 2019Abstract:We consider the recovery of signals from their observations, which are samples of a transform of the signals rather than the signals themselves, by using machine learning (ML). We will develop a theoretical framework to characterize the signals that can be robustly recovered from their observations by an ML algorithm, and establish a Lipschitz condition on signals and observations that is both necessary and sufficient for the existence of a robust recovery. We will compare the Lipschitz condition with the well-known restricted isometry property of the sparse recovery of compressive sensing, and show the former is more general and less restrictive. For linear observations, our work also suggests an ML method in which the output space is reduced to the lowest possible dimension.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge