Data-Driven Continuum Dynamics via Transport-Teleport Duality

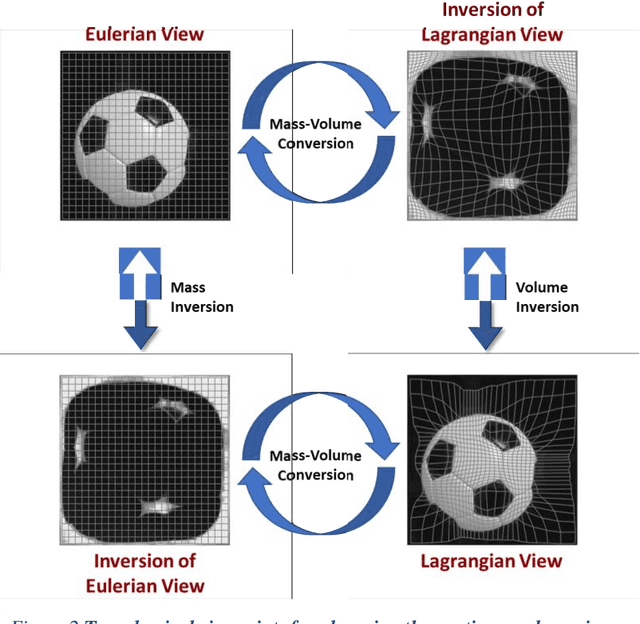
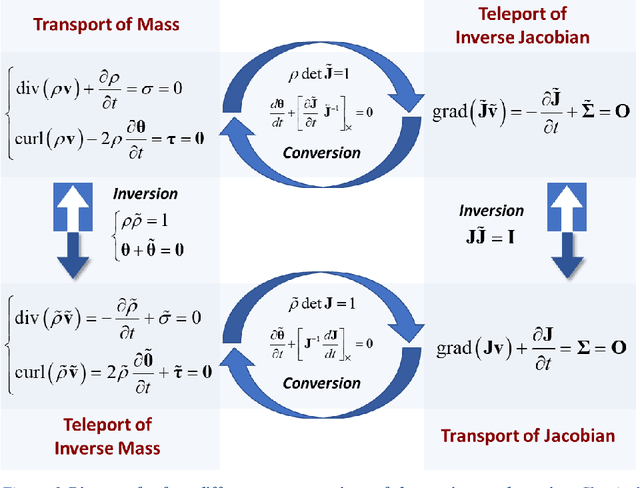
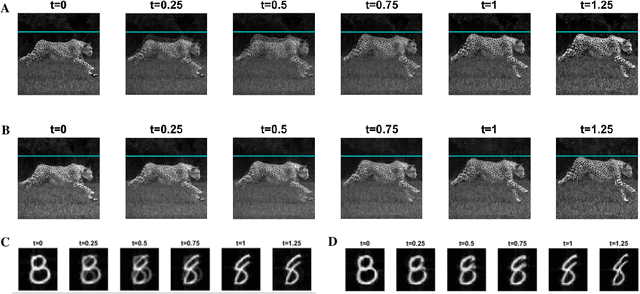
In recent years, machine learning methods have been widely used to study physical systems that are challenging to solve with governing equations. However, most learning architectures do not inherently incorporate conservation laws in the form of continuity equations, and they require dense data to learn the continuum dynamics of conserved quantities. In this study, we propose a mathematical framework for machine learning of transport phenomena. Through the derived involution, the continuity equation becomes a pointwise operation for disappearance and reappearance of a quantity with zero velocity. By modeling the process with sparse observations, we can determine and predict the dynamics of a physical system. The approach does not require the explicit use of governing equations and only depends on observation data.