Eryn : A multi-purpose sampler for Bayesian inference

In recent years, methods for Bayesian inference have been widely used in many different problems in physics where detection and characterization are necessary. Data analysis in gravitational-wave astronomy is a prime example of such a case. Bayesian inference has been very successful because this technique provides a representation of the parameters as a posterior probability distribution, with uncertainties informed by the precision of the experimental measurements. During the last couple of decades, many specific advances have been proposed and employed in order to solve a large variety of different problems. In this work, we present a Markov Chain Monte Carlo (MCMC) algorithm that integrates many of those concepts into a single MCMC package. For this purpose, we have built {\tt Eryn}, a user-friendly and multipurpose toolbox for Bayesian inference, which can be utilized for solving parameter estimation and model selection problems, ranging from simple inference questions, to those with large-scale model variation requiring trans-dimensional MCMC methods, like the LISA global fit problem. In this paper, we describe this sampler package and illustrate its capabilities on a variety of use cases.

Fast methods for training Gaussian processes on large data sets

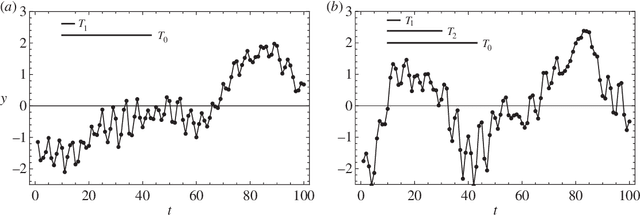
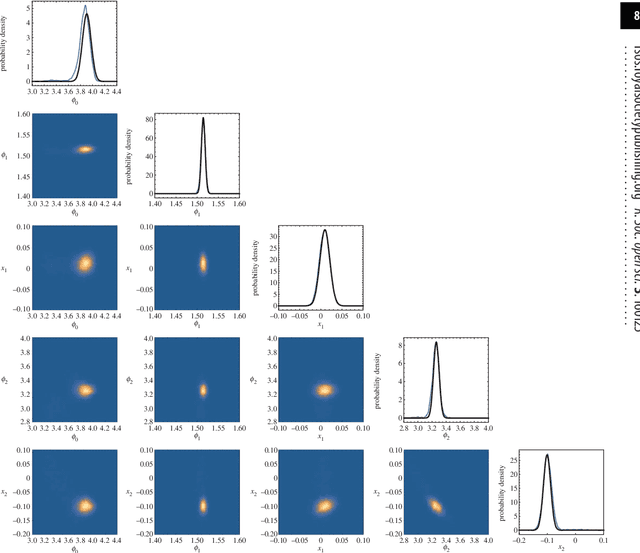
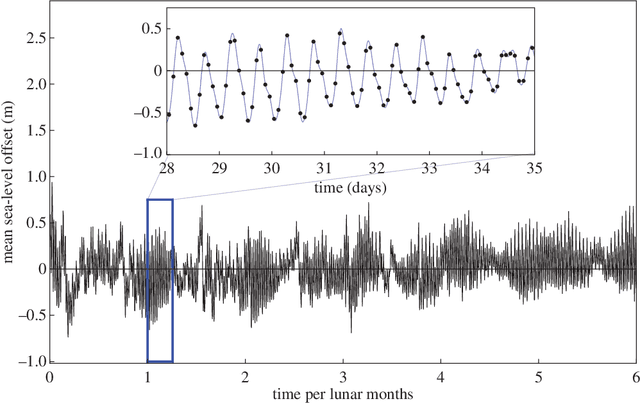
Gaussian process regression (GPR) is a non-parametric Bayesian technique for interpolating or fitting data. The main barrier to further uptake of this powerful tool rests in the computational costs associated with the matrices which arise when dealing with large data sets. Here, we derive some simple results which we have found useful for speeding up the learning stage in the GPR algorithm, and especially for performing Bayesian model comparison between different covariance functions. We apply our techniques to both synthetic and real data and quantify the speed-up relative to using nested sampling to numerically evaluate model evidences.