Soft Checksums to Flag Untrustworthy Machine Learning Surrogate Predictions and Application to Atomic Physics Simulations

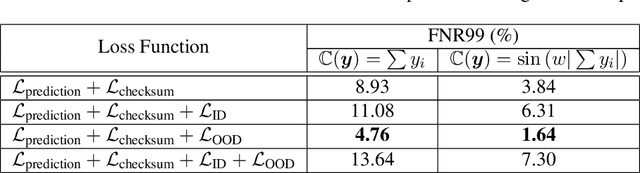
Trained neural networks (NN) are attractive as surrogate models to replace costly calculations in physical simulations, but are often unknowingly applied to states not adequately represented in the training dataset. We present the novel technique of soft checksums for scientific machine learning, a general-purpose method to differentiate between trustworthy predictions with small errors on in-distribution (ID) data points, and untrustworthy predictions with large errors on out-of-distribution (OOD) data points. By adding a check node to the existing output layer, we train the model to learn the chosen checksum function encoded within the NN predictions and show that violations of this function correlate with high prediction errors. As the checksum function depends only on the NN predictions, we can calculate the checksum error for any prediction with a single forward pass, incurring negligible time and memory costs. Additionally, we find that incorporating the checksum function into the loss function and exposing the NN to OOD data points during the training process improves separation between ID and OOD predictions. By applying soft checksums to a physically complex and high-dimensional non-local thermodynamic equilibrium atomic physics dataset, we show that a well-chosen threshold checksum error can effectively separate ID and OOD predictions.

Embedded training of neural-network sub-grid-scale turbulence models

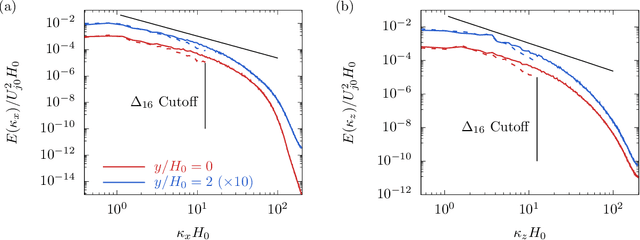
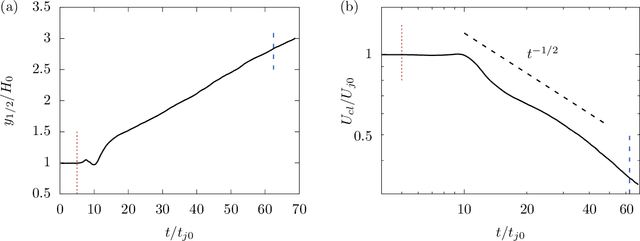
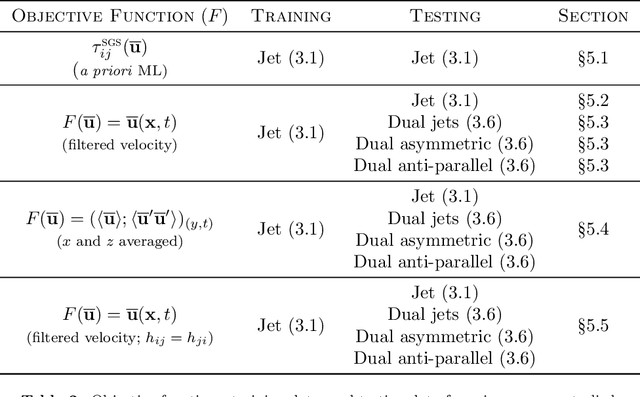
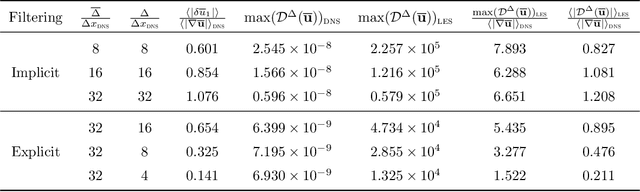
The weights of a deep neural network model are optimized in conjunction with the governing flow equations to provide a model for sub-grid-scale stresses in a temporally developing plane turbulent jet at Reynolds number $Re_0=6\,000$. The objective function for training is first based on the instantaneous filtered velocity fields from a corresponding direct numerical simulation, and the training is by a stochastic gradient descent method, which uses the adjoint Navier--Stokes equations to provide the end-to-end sensitivities of the model weights to the velocity fields. In-sample and out-of-sample testing on multiple dual-jet configurations show that its required mesh density in each coordinate direction for prediction of mean flow, Reynolds stresses, and spectra is half that needed by the dynamic Smagorinsky model for comparable accuracy. The same neural-network model trained directly to match filtered sub-grid-scale stresses -- without the constraint of being embedded within the flow equations during the training -- fails to provide a qualitatively correct prediction. The coupled formulation is generalized to train based only on mean-flow and Reynolds stresses, which are more readily available in experiments. The mean-flow training provides a robust model, which is important, though a somewhat less accurate prediction for the same coarse meshes, as might be anticipated due to the reduced information available for training in this case. The anticipated advantage of the formulation is that the inclusion of resolved physics in the training increases its capacity to extrapolate. This is assessed for the case of passive scalar transport, for which it outperforms established models due to improved mixing predictions.

DPM: A deep learning PDE augmentation method

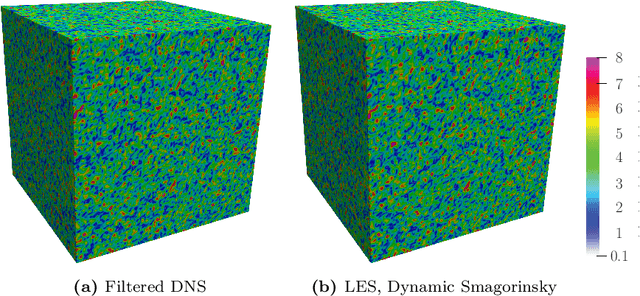
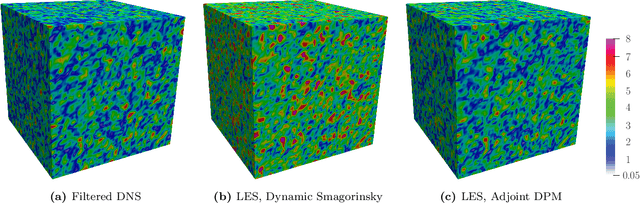
Machine learning for scientific applications faces the challenge of limited data. We propose a framework that leverages a priori known physics to reduce overfitting when training on relatively small datasets. A deep neural network is embedded in a partial differential equation (PDE) that expresses the known physics and learns to describe the corresponding unknown or unrepresented physics from the data. Crafted as such, the neural network can also provide corrections for erroneously represented physics, such as discretization errors associated with the PDE's numerical solution. Once trained, the deep learning PDE model (DPM) can make out-of-sample predictions for new physical parameters, geometries, and boundary conditions. Our approach optimizes over the functional form of the PDE. Estimating the embedded neural network requires optimizing over the entire PDE, which itself is a function of the neural network. Adjoint partial differential equations are used to efficiently calculate the high-dimensional gradient of the objective function with respect to the neural network parameters. A stochastic adjoint method (SAM), similar in spirit to stochastic gradient descent, further accelerates training. The approach is demonstrated and evaluated for turbulence predictions using large-eddy simulation (LES), a filtered version of the Navier--Stokes equation containing unclosed sub-filter-scale terms. The DPM outperforms the widely-used constant-coefficient and dynamic Smagorinsky models, even for filter sizes so large that these established models become qualitatively incorrect. It also significantly outperforms a priori trained models, which do not account for the full PDE. A relaxation of the discrete enforcement of the divergence-free constraint is also considered, instead allowing the DPM to approximately enforce incompressibility physics.