Neural Actor-Critic Methods for Hamilton-Jacobi-Bellman PDEs: Asymptotic Analysis and Numerical Studies

We mathematically analyze and numerically study an actor-critic machine learning algorithm for solving high-dimensional Hamilton-Jacobi-Bellman (HJB) partial differential equations from stochastic control theory. The architecture of the critic (the estimator for the value function) is structured so that the boundary condition is always perfectly satisfied (rather than being included in the training loss) and utilizes a biased gradient which reduces computational cost. The actor (the estimator for the optimal control) is trained by minimizing the integral of the Hamiltonian over the domain, where the Hamiltonian is estimated using the critic. We show that the training dynamics of the actor and critic neural networks converge in a Sobolev-type space to a certain infinite-dimensional ordinary differential equation (ODE) as the number of hidden units in the actor and critic $\rightarrow \infty$. Further, under a convexity-like assumption on the Hamiltonian, we prove that any fixed point of this limit ODE is a solution of the original stochastic control problem. This provides an important guarantee for the algorithm's performance in light of the fact that finite-width neural networks may only converge to a local minimizers (and not optimal solutions) due to the non-convexity of their loss functions. In our numerical studies, we demonstrate that the algorithm can solve stochastic control problems accurately in up to 200 dimensions. In particular, we construct a series of increasingly complex stochastic control problems with known analytic solutions and study the algorithm's numerical performance on them. These problems range from a linear-quadratic regulator equation to highly challenging equations with non-convex Hamiltonians, allowing us to identify and analyze the strengths and limitations of this neural actor-critic method for solving HJB equations.

Global Convergence of Adjoint-Optimized Neural PDEs

Many engineering and scientific fields have recently become interested in modeling terms in partial differential equations (PDEs) with neural networks. The resulting neural-network PDE model, being a function of the neural network parameters, can be calibrated to available data by optimizing over the PDE using gradient descent, where the gradient is evaluated in a computationally efficient manner by solving an adjoint PDE. These neural-network PDE models have emerged as an important research area in scientific machine learning. In this paper, we study the convergence of the adjoint gradient descent optimization method for training neural-network PDE models in the limit where both the number of hidden units and the training time tend to infinity. Specifically, for a general class of nonlinear parabolic PDEs with a neural network embedded in the source term, we prove convergence of the trained neural-network PDE solution to the target data (i.e., a global minimizer). The global convergence proof poses a unique mathematical challenge that is not encountered in finite-dimensional neural network convergence analyses due to (1) the neural network training dynamics involving a non-local neural network kernel operator in the infinite-width hidden layer limit where the kernel lacks a spectral gap for its eigenvalues and (2) the nonlinearity of the limit PDE system, which leads to a non-convex optimization problem, even in the infinite-width hidden layer limit (unlike in typical neual network training cases where the optimization problem becomes convex in the large neuron limit). The theoretical results are illustrated and empirically validated by numerical studies.

Convergence Analysis of Real-time Recurrent Learning (RTRL) for a class of Recurrent Neural Networks

Recurrent neural networks (RNNs) are commonly trained with the truncated backpropagation-through-time (TBPTT) algorithm. For the purposes of computational tractability, the TBPTT algorithm truncates the chain rule and calculates the gradient on a finite block of the overall data sequence. Such approximation could lead to significant inaccuracies, as the block length for the truncated backpropagation is typically limited to be much smaller than the overall sequence length. In contrast, Real-time recurrent learning (RTRL) is an online optimization algorithm which asymptotically follows the true gradient of the loss on the data sequence as the number of sequence time steps $t \rightarrow \infty$. RTRL forward propagates the derivatives of the RNN hidden/memory units with respect to the parameters and, using the forward derivatives, performs online updates of the parameters at each time step in the data sequence. RTRL's online forward propagation allows for exact optimization over extremely long data sequences, although it can be computationally costly for models with large numbers of parameters. We prove convergence of the RTRL algorithm for a class of RNNs. The convergence analysis establishes a fixed point for the joint distribution of the data sequence, RNN hidden layer, and the RNN hidden layer forward derivatives as the number of data samples from the sequence and the number of training steps tend to infinity. We prove convergence of the RTRL algorithm to a stationary point of the loss. Numerical studies illustrate our theoretical results. One potential application area for RTRL is the analysis of financial data, which typically involve long time series and models with small to medium numbers of parameters. This makes RTRL computationally tractable and a potentially appealing optimization method for training models. Thus, we include an example of RTRL applied to limit order book data.

Weak Convergence Analysis of Online Neural Actor-Critic Algorithms

We prove that a single-layer neural network trained with the online actor critic algorithm converges in distribution to a random ordinary differential equation (ODE) as the number of hidden units and the number of training steps $\rightarrow \infty$. In the online actor-critic algorithm, the distribution of the data samples dynamically changes as the model is updated, which is a key challenge for any convergence analysis. We establish the geometric ergodicity of the data samples under a fixed actor policy. Then, using a Poisson equation, we prove that the fluctuations of the model updates around the limit distribution due to the randomly-arriving data samples vanish as the number of parameter updates $\rightarrow \infty$. Using the Poisson equation and weak convergence techniques, we prove that the actor neural network and critic neural network converge to the solutions of a system of ODEs with random initial conditions. Analysis of the limit ODE shows that the limit critic network will converge to the true value function, which will provide the actor an asymptotically unbiased estimate of the policy gradient. We then prove that the limit actor network will converge to a stationary point.

Kernel Limit of Recurrent Neural Networks Trained on Ergodic Data Sequences

Mathematical methods are developed to characterize the asymptotics of recurrent neural networks (RNN) as the number of hidden units, data samples in the sequence, hidden state updates, and training steps simultaneously grow to infinity. In the case of an RNN with a simplified weight matrix, we prove the convergence of the RNN to the solution of an infinite-dimensional ODE coupled with the fixed point of a random algebraic equation. The analysis requires addressing several challenges which are unique to RNNs. In typical mean-field applications (e.g., feedforward neural networks), discrete updates are of magnitude $\mathcal{O}(\frac{1}{N})$ and the number of updates is $\mathcal{O}(N)$. Therefore, the system can be represented as an Euler approximation of an appropriate ODE/PDE, which it will converge to as $N \rightarrow \infty$. However, the RNN hidden layer updates are $\mathcal{O}(1)$. Therefore, RNNs cannot be represented as a discretization of an ODE/PDE and standard mean-field techniques cannot be applied. Instead, we develop a fixed point analysis for the evolution of the RNN memory states, with convergence estimates in terms of the number of update steps and the number of hidden units. The RNN hidden layer is studied as a function in a Sobolev space, whose evolution is governed by the data sequence (a Markov chain), the parameter updates, and its dependence on the RNN hidden layer at the previous time step. Due to the strong correlation between updates, a Poisson equation must be used to bound the fluctuations of the RNN around its limit equation. These mathematical methods give rise to the neural tangent kernel (NTK) limits for RNNs trained on data sequences as the number of data samples and size of the neural network grow to infinity.

Global Convergence of Deep Galerkin and PINNs Methods for Solving Partial Differential Equations

Numerically solving high-dimensional partial differential equations (PDEs) is a major challenge. Conventional methods, such as finite difference methods, are unable to solve high-dimensional PDEs due to the curse-of-dimensionality. A variety of deep learning methods have been recently developed to try and solve high-dimensional PDEs by approximating the solution using a neural network. In this paper, we prove global convergence for one of the commonly-used deep learning algorithms for solving PDEs, the Deep Galerkin Method (DGM). DGM trains a neural network approximator to solve the PDE using stochastic gradient descent. We prove that, as the number of hidden units in the single-layer network goes to infinity (i.e., in the ``wide network limit"), the trained neural network converges to the solution of an infinite-dimensional linear ordinary differential equation (ODE). The PDE residual of the limiting approximator converges to zero as the training time $\rightarrow \infty$. Under mild assumptions, this convergence also implies that the neural network approximator converges to the solution of the PDE. A closely related class of deep learning methods for PDEs is Physics Informed Neural Networks (PINNs). Using the same mathematical techniques, we can prove a similar global convergence result for the PINN neural network approximators. Both proofs require analyzing a kernel function in the limit ODE governing the evolution of the limit neural network approximator. A key technical challenge is that the kernel function, which is a composition of the PDE operator and the neural tangent kernel (NTK) operator, lacks a spectral gap, therefore requiring a careful analysis of its properties.

Dynamic Deep Learning LES Closures: Online Optimization With Embedded DNS

Deep learning (DL) has recently emerged as a candidate for closure modeling of large-eddy simulation (LES) of turbulent flows. High-fidelity training data is typically limited: it is computationally costly (or even impossible) to numerically generate at high Reynolds numbers, while experimental data is also expensive to produce and might only include sparse/aggregate flow measurements. Thus, only a relatively small number of geometries and physical regimes will realistically be included in any training dataset. Limited data can lead to overfitting and therefore inaccurate predictions for geometries and physical regimes that are different from the training cases. We develop a new online training method for deep learning closure models in LES which seeks to address this challenge. The deep learning closure model is dynamically trained during a large-eddy simulation (LES) calculation using embedded direct numerical simulation (DNS) data. That is, in a small subset of the domain, the flow is computed at DNS resolutions in concert with the LES prediction. The closure model then adjusts its approximation to the unclosed terms using data from the embedded DNS. Consequently, the closure model is trained on data from the exact geometry/physical regime of the prediction at hand. An online optimization algorithm is developed to dynamically train the deep learning closure model in the coupled, LES-embedded DNS calculation.

Deep Learning Closure Models for Large-Eddy Simulation of Flows around Bluff Bodies

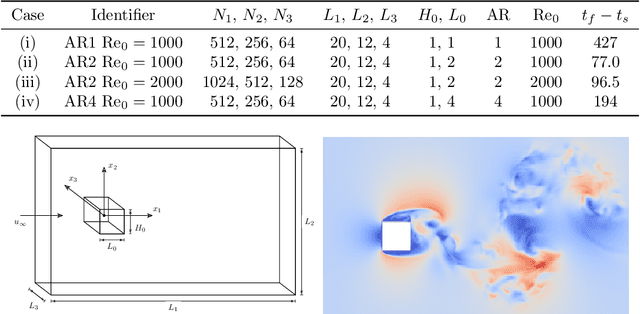
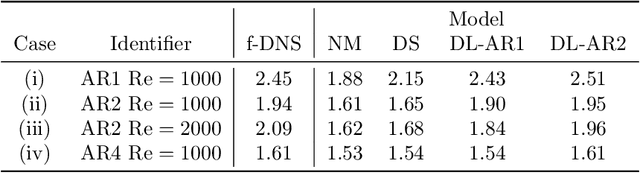
A deep learning (DL) closure model for large-eddy simulation (LES) is developed and evaluated for incompressible flows around a rectangular cylinder at moderate Reynolds numbers. Near-wall flow simulation remains a central challenge in aerodynamic modeling: RANS predictions of separated flows are often inaccurate, while LES can require prohibitively small near-wall mesh sizes. The DL-LES model is trained using adjoint PDE optimization methods to match, as closely as possible, direct numerical simulation (DNS) data. It is then evaluated out-of-sample (i.e., for new aspect ratios and Reynolds numbers not included in the training data) and compared against a standard LES model (the dynamic Smagorinsky model). The DL-LES model outperforms dynamic Smagorinsky and is able to achieve accurate LES predictions on a relatively coarse mesh (downsampled from the DNS grid by a factor of four in each Cartesian direction). We study the accuracy of the DL-LES model for predicting the drag coefficient, mean flow, and Reynolds stress. A crucial challenge is that the LES quantities of interest are the steady-state flow statistics; for example, the time-averaged mean velocity $\bar{u}(x) = \displaystyle \lim_{t \rightarrow \infty} \frac{1}{t} \int_0^t u(s,x) ds$. Calculating the steady-state flow statistics therefore requires simulating the DL-LES equations over a large number of flow times through the domain; it is a non-trivial question whether an unsteady partial differential equation model whose functional form is defined by a deep neural network can remain stable and accurate on $t \in [0, \infty)$. Our results demonstrate that the DL-LES model is accurate and stable over large physical time spans, enabling the estimation of the steady-state statistics for the velocity, fluctuations, and drag coefficient of turbulent flows around bluff bodies relevant to aerodynamic applications.

A Forward Propagation Algorithm for Online Optimization of Nonlinear Stochastic Differential Equations

Optimizing over the stationary distribution of stochastic differential equations (SDEs) is computationally challenging. A new forward propagation algorithm has been recently proposed for the online optimization of SDEs. The algorithm solves an SDE, derived using forward differentiation, which provides a stochastic estimate for the gradient. The algorithm continuously updates the SDE model's parameters and the gradient estimate simultaneously. This paper studies the convergence of the forward propagation algorithm for nonlinear dissipative SDEs. We leverage the ergodicity of this class of nonlinear SDEs to characterize the convergence rate of the transition semi-group and its derivatives. Then, we prove bounds on the solution of a Poisson partial differential equation (PDE) for the expected time integral of the algorithm's stochastic fluctuations around the direction of steepest descent. We then re-write the algorithm using the PDE solution, which allows us to characterize the parameter evolution around the direction of steepest descent. Our main result is a convergence theorem for the forward propagation algorithm for nonlinear dissipative SDEs.

Neural Q-learning for solving elliptic PDEs

Solving high-dimensional partial differential equations (PDEs) is a major challenge in scientific computing. We develop a new numerical method for solving elliptic-type PDEs by adapting the Q-learning algorithm in reinforcement learning. Our "Q-PDE" algorithm is mesh-free and therefore has the potential to overcome the curse of dimensionality. Using a neural tangent kernel (NTK) approach, we prove that the neural network approximator for the PDE solution, trained with the Q-PDE algorithm, converges to the trajectory of an infinite-dimensional ordinary differential equation (ODE) as the number of hidden units $\rightarrow \infty$. For monotone PDE (i.e. those given by monotone operators, which may be nonlinear), despite the lack of a spectral gap in the NTK, we then prove that the limit neural network, which satisfies the infinite-dimensional ODE, converges in $L^2$ to the PDE solution as the training time $\rightarrow \infty$. More generally, we can prove that any fixed point of the wide-network limit for the Q-PDE algorithm is a solution of the PDE (not necessarily under the monotone condition). The numerical performance of the Q-PDE algorithm is studied for several elliptic PDEs.