DPM: A deep learning PDE augmentation method

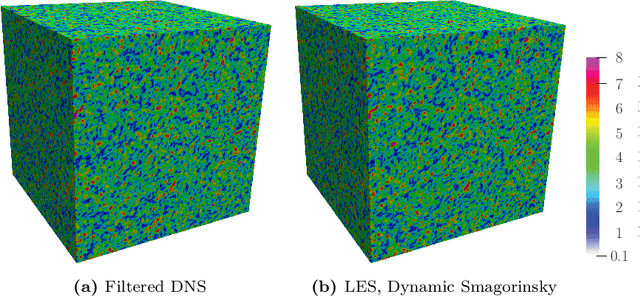
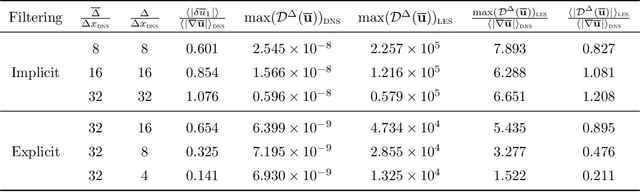
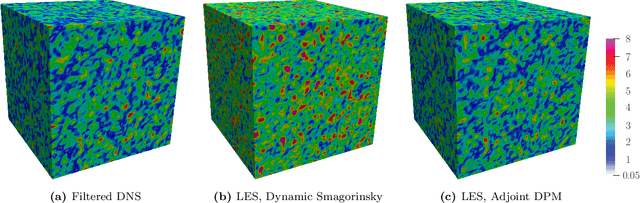
Machine learning for scientific applications faces the challenge of limited data. We propose a framework that leverages a priori known physics to reduce overfitting when training on relatively small datasets. A deep neural network is embedded in a partial differential equation (PDE) that expresses the known physics and learns to describe the corresponding unknown or unrepresented physics from the data. Crafted as such, the neural network can also provide corrections for erroneously represented physics, such as discretization errors associated with the PDE's numerical solution. Once trained, the deep learning PDE model (DPM) can make out-of-sample predictions for new physical parameters, geometries, and boundary conditions. Our approach optimizes over the functional form of the PDE. Estimating the embedded neural network requires optimizing over the entire PDE, which itself is a function of the neural network. Adjoint partial differential equations are used to efficiently calculate the high-dimensional gradient of the objective function with respect to the neural network parameters. A stochastic adjoint method (SAM), similar in spirit to stochastic gradient descent, further accelerates training. The approach is demonstrated and evaluated for turbulence predictions using large-eddy simulation (LES), a filtered version of the Navier--Stokes equation containing unclosed sub-filter-scale terms. The DPM outperforms the widely-used constant-coefficient and dynamic Smagorinsky models, even for filter sizes so large that these established models become qualitatively incorrect. It also significantly outperforms a priori trained models, which do not account for the full PDE. A relaxation of the discrete enforcement of the divergence-free constraint is also considered, instead allowing the DPM to approximately enforce incompressibility physics.