Reinforcement-learning calibration of coherent-state receivers on variable-loss optical channels

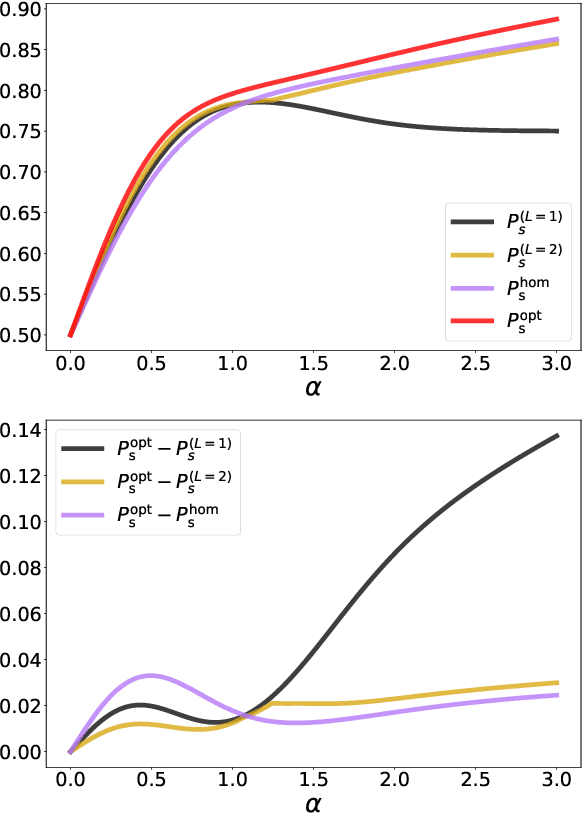
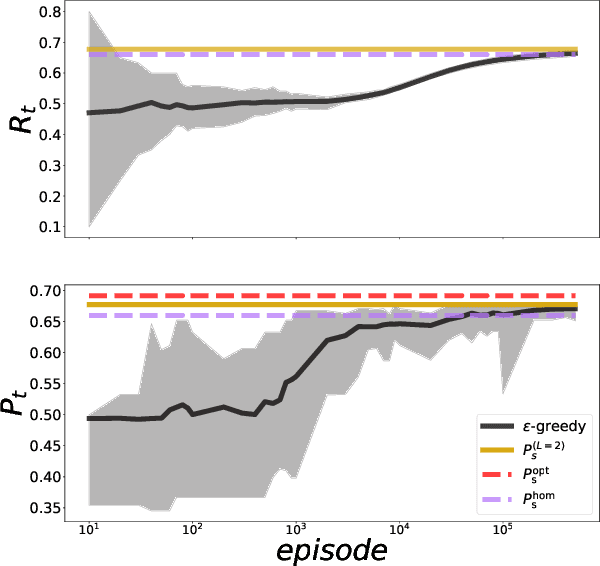
We study the problem of calibrating a quantum receiver for optical coherent states when transmitted on a quantum optical channel with variable transmissivity, a common model for long-distance optical-fiber and free/deep-space optical communication. We optimize the error probability of legacy adaptive receivers, such as Kennedy's and Dolinar's, on average with respect to the channel transmissivity distribution. We then compare our results with the ultimate error probability attainable by a general quantum device, computing the Helstrom bound for mixtures of coherent-state hypotheses, for the first time to our knowledge, and with homodyne measurements. With these tools, we first analyze the simplest case of two different transmissivity values; we find that the strategies adopted by adaptive receivers exhibit strikingly new features as the difference between the two transmissivities increases. Finally, we employ a recently introduced library of shallow reinforcement learning methods, demonstrating that an intelligent agent can learn the optimal receiver setup from scratch by training on repeated communication episodes on the channel with variable transmissivity and receiving rewards if the coherent-state message is correctly identified.

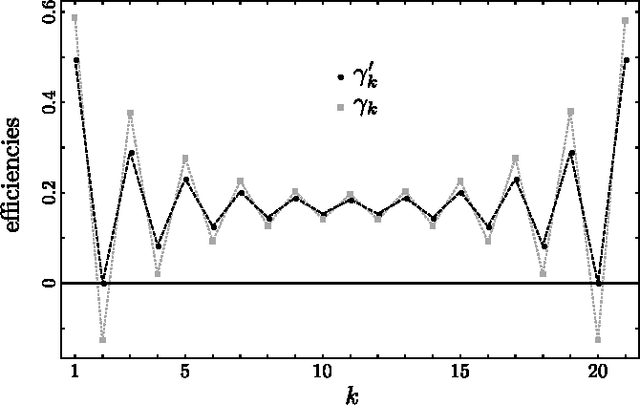
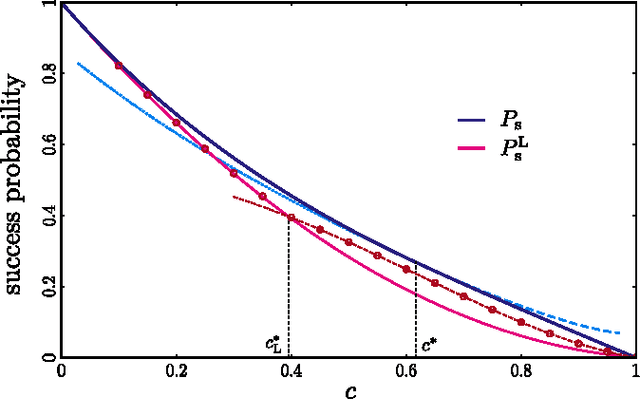
Exact Identification of a Quantum Change Point

The detection of change points is a pivotal task in statistical analysis. In the quantum realm, it is a new primitive where one aims at identifying the point where a source that supposedly prepares a sequence of particles in identical quantum states starts preparing a mutated one. We obtain the optimal procedure to identify the change point with certainty---naturally at the price of having a certain probability of getting an inconclusive answer. We obtain the analytical form of the optimal probability of successful identification for any length of the particle sequence. We show that the conditional success probabilities of identifying each possible change point show an unexpected oscillatory behaviour. We also discuss local (online) protocols and compare them with the optimal procedure.