Efficient Winograd Convolution via Integer Arithmetic

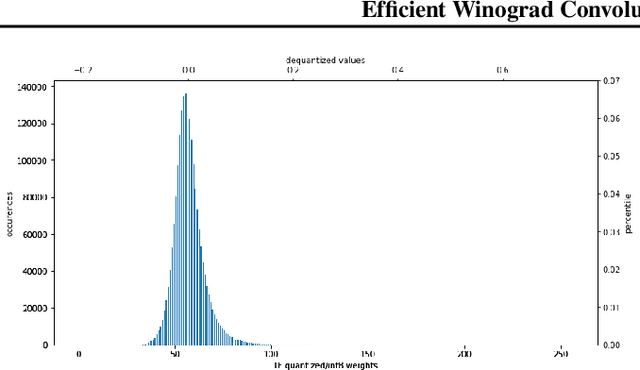
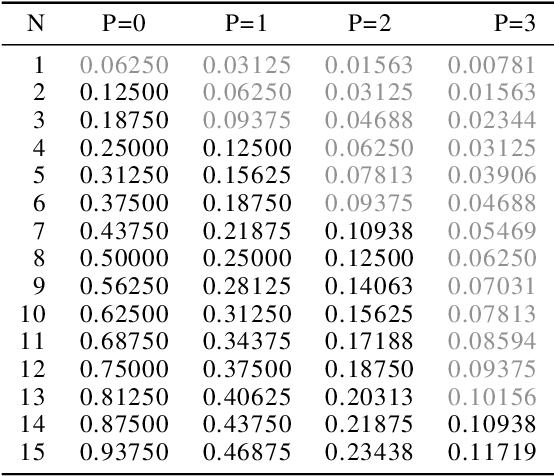
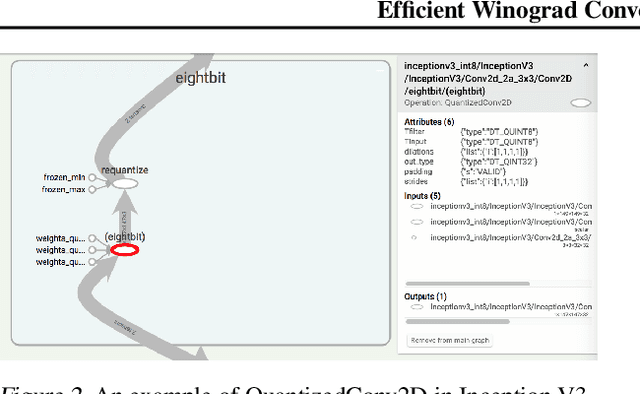
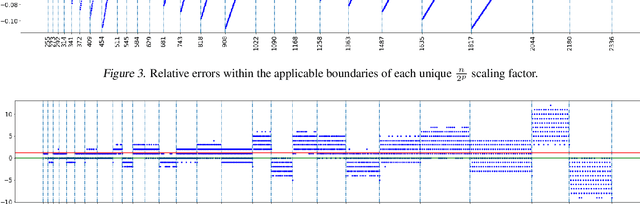
Convolution is the core operation for many deep neural networks. The Winograd convolution algorithms have been shown to accelerate the widely-used small convolution sizes. Quantized neural networks can effectively reduce model sizes and improve inference speed, which leads to a wide variety of kernels and hardware accelerators that work with integer data. The state-of-the-art Winograd algorithms pose challenges for efficient implementation and execution by the integer kernels and accelerators. We introduce a new class of Winograd algorithms by extending the construction to the field of complex and propose optimizations that reduce the number of general multiplications. The new algorithm achieves an arithmetic complexity reduction of $3.13$x over the direct method and an efficiency gain up to $17.37\%$ over the rational algorithms. Furthermore, we design and implement an integer-based filter scaling scheme to effectively reduce the filter bit width by $30.77\%$ without any significant accuracy loss.

FPGA-Based CNN Inference Accelerator Synthesized from Multi-Threaded C Software

A deep-learning inference accelerator is synthesized from a C-language software program parallelized with Pthreads. The software implementation uses the well-known producer/consumer model with parallel threads interconnected by FIFO queues. The LegUp high-level synthesis (HLS) tool synthesizes threads into parallel FPGA hardware, translating software parallelism into spatial parallelism. A complete system is generated where convolution, pooling and padding are realized in the synthesized accelerator, with remaining tasks executing on an embedded ARM processor. The accelerator incorporates reduced precision, and a novel approach for zero-weight-skipping in convolution. On a mid-sized Intel Arria 10 SoC FPGA, peak performance on VGG-16 is 138 effective GOPS.