Efficient Winograd Convolution via Integer Arithmetic

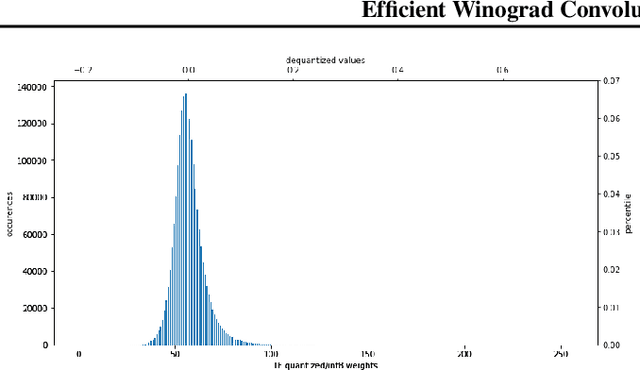
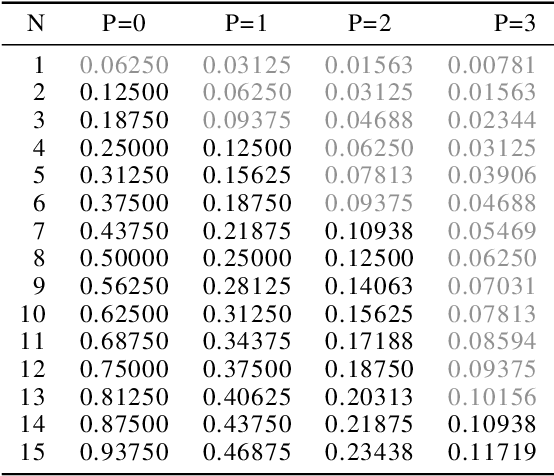
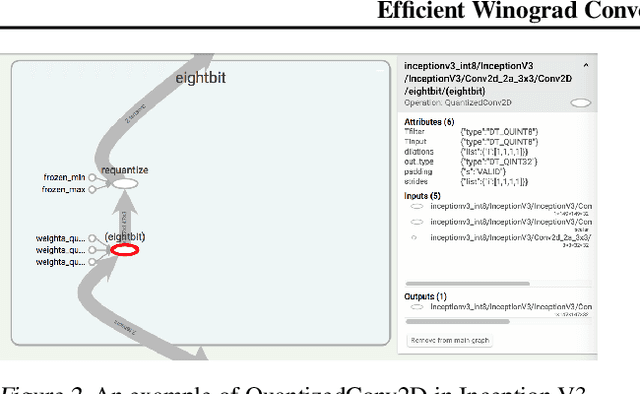
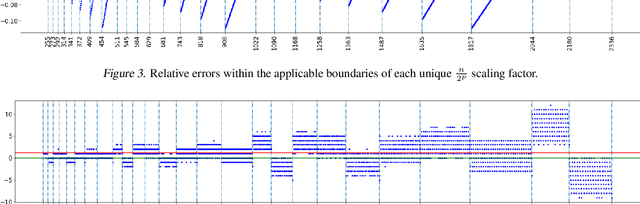
Convolution is the core operation for many deep neural networks. The Winograd convolution algorithms have been shown to accelerate the widely-used small convolution sizes. Quantized neural networks can effectively reduce model sizes and improve inference speed, which leads to a wide variety of kernels and hardware accelerators that work with integer data. The state-of-the-art Winograd algorithms pose challenges for efficient implementation and execution by the integer kernels and accelerators. We introduce a new class of Winograd algorithms by extending the construction to the field of complex and propose optimizations that reduce the number of general multiplications. The new algorithm achieves an arithmetic complexity reduction of $3.13$x over the direct method and an efficiency gain up to $17.37\%$ over the rational algorithms. Furthermore, we design and implement an integer-based filter scaling scheme to effectively reduce the filter bit width by $30.77\%$ without any significant accuracy loss.