Fractal Descriptors of Texture Images Based on the Triangular Prism Dimension

This work presents a novel descriptor for texture images based on fractal geometry and its application to image analysis. The descriptors are provided by estimating the triangular prism fractal dimension under different scales with a weight exponential parameter, followed by dimensionality reduction using Karhunen-Lo\`{e}ve transform. The efficiency of the proposed descriptors is tested on two well-known texture data sets, that is, Brodatz and Vistex, both for classification and image retrieval. The novel method is also tested concerning invariances in situations when the textures are rotated or affected by Gaussian noise. The obtained results outperform other classical and state-of-the-art descriptors in the literature and demonstrate the power of the triangular descriptors in these tasks, suggesting their use in practical applications of image analysis based on texture features.

Discrete Schroedinger Transform For Texture Recognition

This work presents a new procedure to extract features of grey-level texture images based on the discrete Schroedinger transform. This is a non-linear transform where the image is mapped as the initial probability distribution of a wave function and such distribution evolves in time following the Schroedinger equation from Quantum Mechanics. The features are provided by statistical moments of the distribution measured at different times. The proposed method is applied to the classification of three databases of textures used for benchmark and compared to other well-known texture descriptors in the literature, such as textons, local binary patterns, multifractals, among others. All of them are outperformed by the proposed method in terms of percentage of images correctly classified. The proposal is also applied to the identification of plant species using scanned images of leaves and again it outperforms other texture methods. A test with images affected by Gaussian and "salt \& pepper" noise is also carried out, also with the best performance achieved by the Schroedinger descriptors.

Texture analysis by multi-resolution fractal descriptors

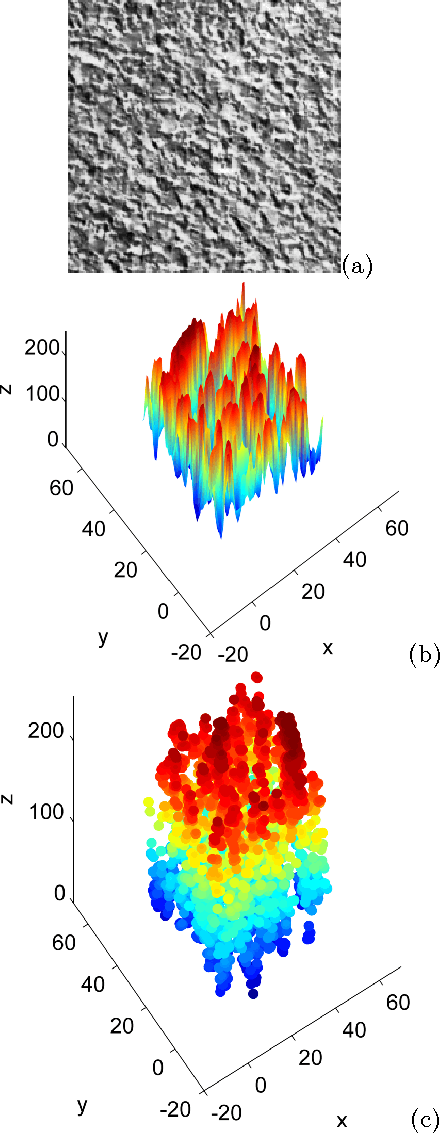
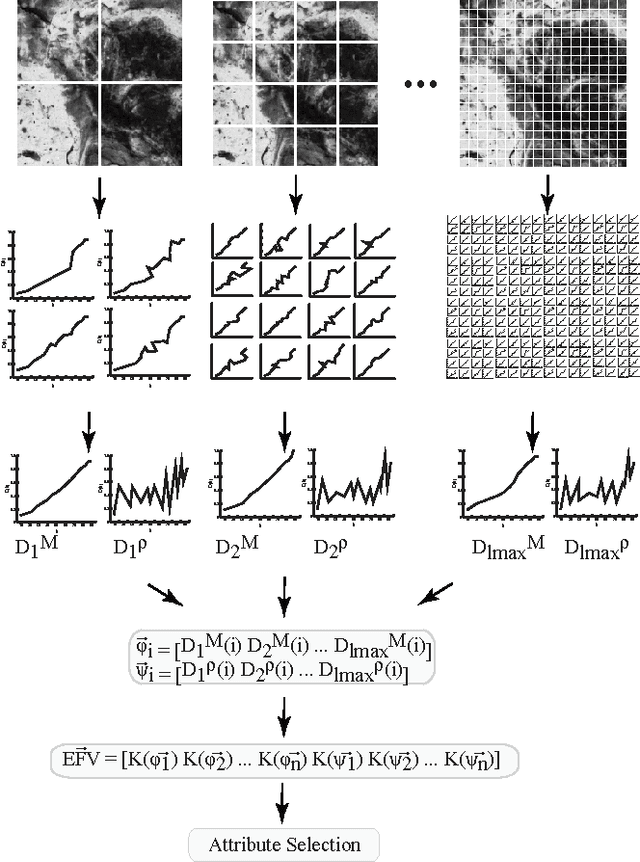
This work proposes a texture descriptor based on fractal theory. The method is based on the Bouligand-Minkowski descriptors. We decompose the original image recursively into 4 equal parts. In each recursion step, we estimate the average and the deviation of the Bouligand-Minkowski descriptors computed over each part. Thus, we extract entropy features from both average and deviation. The proposed descriptors are provided by the concatenation of such measures. The method is tested in a classification experiment under well known datasets, that is, Brodatz and Vistex. The results demonstrate that the proposed technique achieves better results than classical and state-of-the-art texture descriptors, such as Gabor-wavelets and co-occurrence matrix.

Enhancing fractal descriptors on images by combining boundary and interior of Minkowski dilation

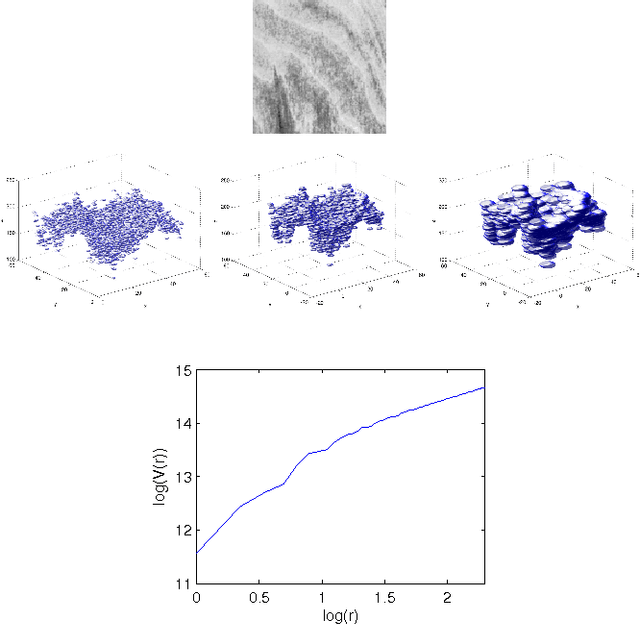
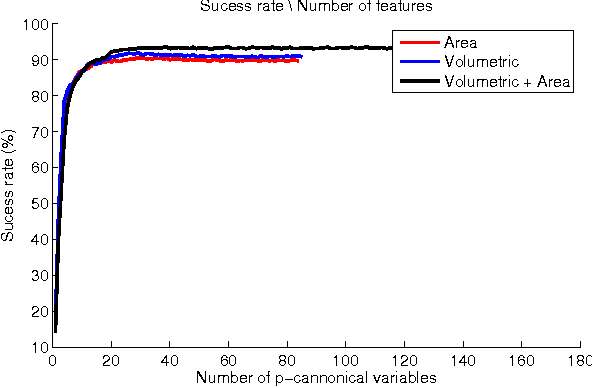
This work proposes to obtain novel fractal descriptors from gray-level texture images by combining information from interior and boundary measures of the Minkowski dilation applied to the texture surface. At first, the image is converted into a surface where the height of each point is the gray intensity of the respective pixel in that position in the image. Thus, this surface is morphologically dilated by spheres. The radius of such spheres is ranged within an interval and the volume and the external area of the dilated structure are computed for each radius. The final descriptors are given by such measures concatenated and subject to a canonical transform to reduce the dimensionality. The proposal is an enhancement to the classical Bouligand-Minkowski fractal descriptors, where only the volume (interior) information is considered. As different structures may have the same volume, but not the same area, the proposal yields to more rich descriptors as confirmed by results on the classification of benchmark databases.

Gabor wavelets combined with volumetric fractal dimension applied to texture analysis

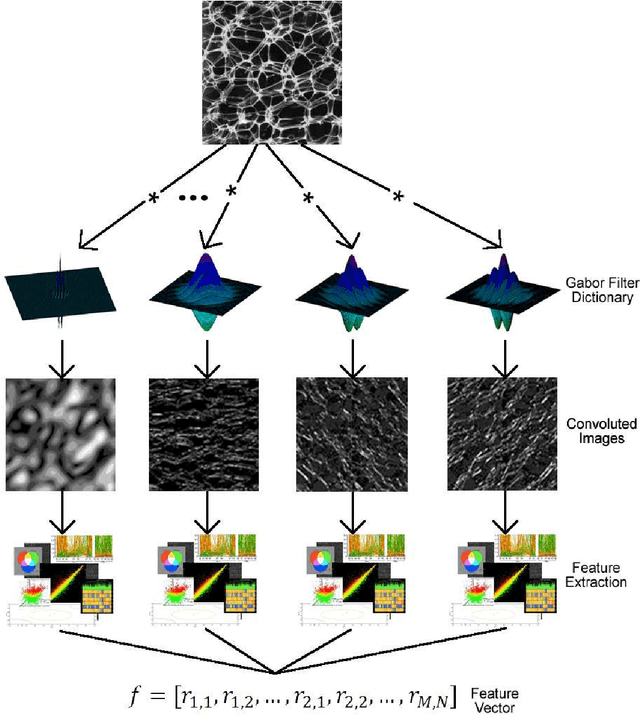
Texture analysis and classification remain as one of the biggest challenges for the field of computer vision and pattern recognition. On this matter, Gabor wavelets has proven to be a useful technique to characterize distinctive texture patterns. However, most of the approaches used to extract descriptors of the Gabor magnitude space usually fail in representing adequately the richness of detail present into a unique feature vector. In this paper, we propose a new method to enhance the Gabor wavelets process extracting a fractal signature of the magnitude spaces. Each signature is reduced using a canonical analysis function and concatenated to form the final feature vector. Experiments were conducted on several texture image databases to prove the power and effectiveness of the proposed method. Results obtained shown that this method outperforms other early proposed method, creating a more reliable technique for texture feature extraction.

Multiscale Fractal Descriptors Applied to Nanoscale Images

This work proposes the application of fractal descriptors to the analysis of nanoscale materials under different experimental conditions. We obtain descriptors for images from the sample applying a multiscale transform to the calculation of fractal dimension of a surface map of such image. Particularly, we have used the}Bouligand-Minkowski fractal dimension. We applied these descriptors to discriminate between two titanium oxide films prepared under different experimental conditions. Results demonstrate the discrimination power of proposed descriptors in such kind of application.

Shape analysis using fractal dimension: a curvature based approach

The present work shows a novel fractal dimension method for shape analysis. The proposed technique extracts descriptors from the shape by applying a multiscale approach to the calculus of the fractal dimension of that shape. The fractal dimension is obtained by the application of the curvature scale-space technique to the original shape. Through the application of a multiscale transform to the dimension calculus, it is obtained a set of numbers (descriptors) capable of describing with a high precision the shape in analysis. The obtained descriptors are validated in a classification process. The results demonstrate that the novel technique provides descriptors highly reliable, confirming the precision of the proposed method.