Jionghua "Judy" Jin
WOOD: Wasserstein-based Out-of-Distribution Detection
Dec 13, 2021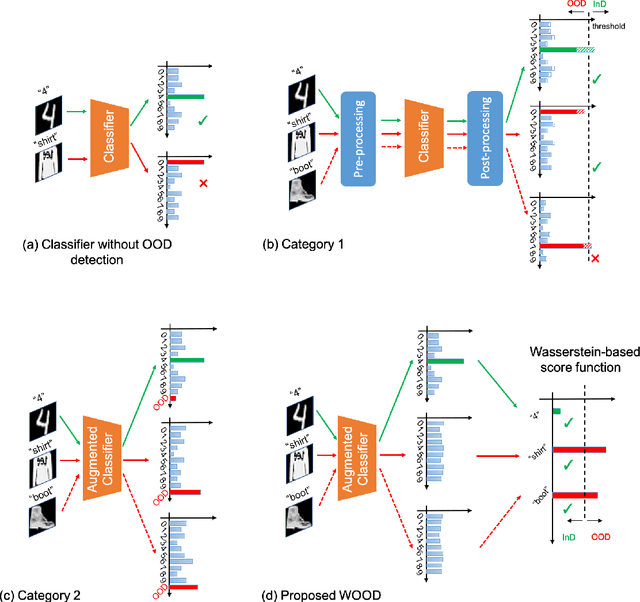

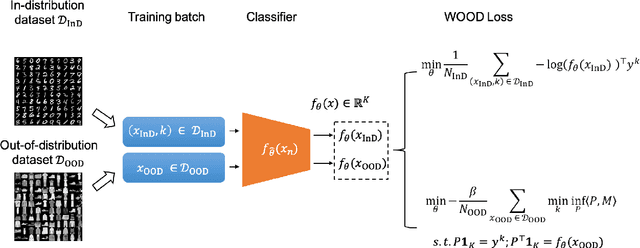
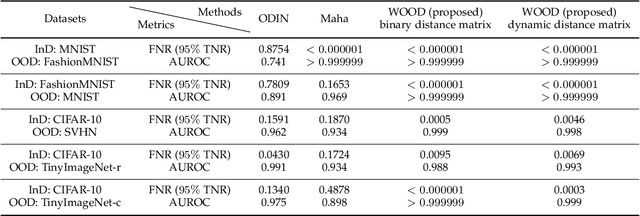
Abstract:The training and test data for deep-neural-network-based classifiers are usually assumed to be sampled from the same distribution. When part of the test samples are drawn from a distribution that is sufficiently far away from that of the training samples (a.k.a. out-of-distribution (OOD) samples), the trained neural network has a tendency to make high confidence predictions for these OOD samples. Detection of the OOD samples is critical when training a neural network used for image classification, object detection, etc. It can enhance the classifier's robustness to irrelevant inputs, and improve the system resilience and security under different forms of attacks. Detection of OOD samples has three main challenges: (i) the proposed OOD detection method should be compatible with various architectures of classifiers (e.g., DenseNet, ResNet), without significantly increasing the model complexity and requirements on computational resources; (ii) the OOD samples may come from multiple distributions, whose class labels are commonly unavailable; (iii) a score function needs to be defined to effectively separate OOD samples from in-distribution (InD) samples. To overcome these challenges, we propose a Wasserstein-based out-of-distribution detection (WOOD) method. The basic idea is to define a Wasserstein-distance-based score that evaluates the dissimilarity between a test sample and the distribution of InD samples. An optimization problem is then formulated and solved based on the proposed score function. The statistical learning bound of the proposed method is investigated to guarantee that the loss value achieved by the empirical optimizer approximates the global optimum. The comparison study results demonstrate that the proposed WOOD consistently outperforms other existing OOD detection methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge