Probabilistic Inference in the Era of Tensor Networks and Differential Programming

Probabilistic inference is a fundamental task in modern machine learning. Recent advances in tensor network (TN) contraction algorithms have enabled the development of better exact inference methods. However, many common inference tasks in probabilistic graphical models (PGMs) still lack corresponding TN-based adaptations. In this work, we advance the connection between PGMs and TNs by formulating and implementing tensor-based solutions for the following inference tasks: (i) computing the partition function, (ii) computing the marginal probability of sets of variables in the model, (iii) determining the most likely assignment to a set of variables, and (iv) the same as (iii) but after having marginalized a different set of variables. We also present a generalized method for generating samples from a learned probability distribution. Our work is motivated by recent technical advances in the fields of quantum circuit simulation, quantum many-body physics, and statistical physics. Through an experimental evaluation, we demonstrate that the integration of these quantum technologies with a series of algorithms introduced in this study significantly improves the effectiveness of existing methods for solving probabilistic inference tasks.

Differentiate Everything with a Reversible Programming Language

This paper considers the source-to-source automatic differentiation (AD) in a reversible language. We start by reviewing the limitations of traditional AD frameworks. To solve the issues in these frameworks, we developed a reversible eDSL NiLang in Julia that can differentiate a general program while being compatible with Julia's ecosystem. It empowers users the flexibility to tradeoff time, space, and energy so that one can use it to obtain gradients and Hessians ranging for elementary mathematical functions, sparse matrix operations, and linear algebra that are widely used in scientific programming. We demonstrate that a source-to-source AD framework can achieve the state-of-the-art performance by showing and benchmarking several examples. Finally, we will discuss the challenges that we face towards rigorous reversible programming, mainly from the instruction and hardware perspective.

Learning and Inference on Generative Adversarial Quantum Circuits

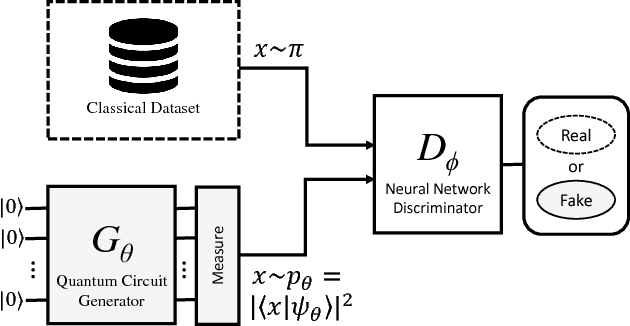
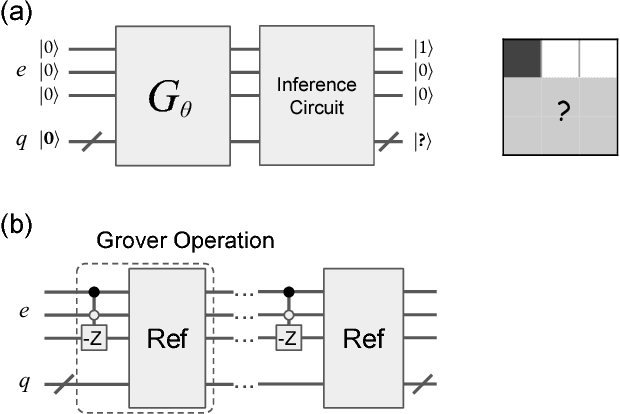
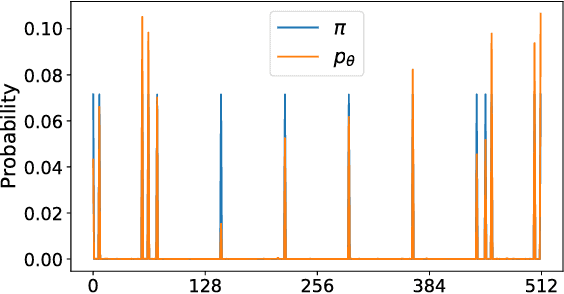
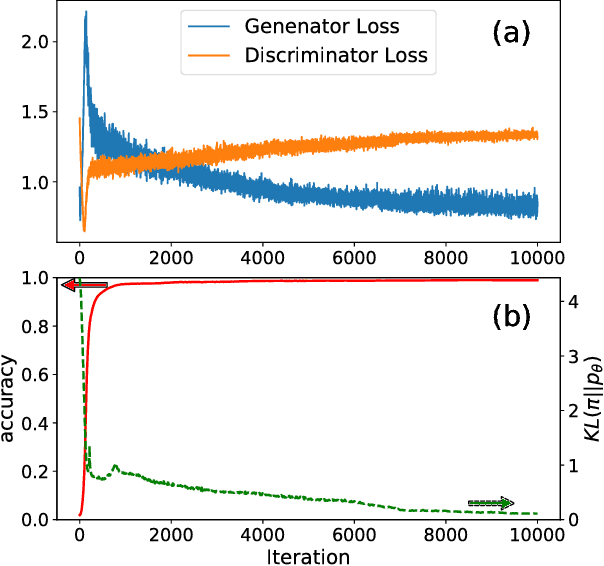
Quantum mechanics is inherently probabilistic in light of Born's rule. Using quantum circuits as probabilistic generative models for classical data exploits their superior expressibility and efficient direct sampling ability. However, training of quantum circuits can be more challenging compared to classical neural networks due to lack of efficient differentiable learning algorithm. We devise an adversarial quantum-classical hybrid training scheme via coupling a quantum circuit generator and a classical neural network discriminator together. After training, the quantum circuit generative model can infer missing data with quadratic speed up via amplitude amplification. We numerically simulate the learning and inference of generative adversarial quantum circuit using the prototypical Bars-and-Stripes dataset. Generative adversarial quantum circuits is a fresh approach to machine learning which may enjoy the practically useful quantum advantage on near-term quantum devices.

Differentiable Learning of Quantum Circuit Born Machine

Quantum circuit Born machines are generative models which represent the probability distribution of classical dataset as quantum pure states. Computational complexity considerations of the quantum sampling problem suggest that the quantum circuits exhibit stronger expressibility compared to classical neural networks. One can efficiently draw samples from the quantum circuits via projective measurements on qubits. However, similar to the leading implicit generative models in deep learning, such as the generative adversarial networks, the quantum circuits cannot provide the likelihood of the generated samples, which poses a challenge to the training. We devise an efficient gradient-based learning algorithm for the quantum circuit Born machine by minimizing the kerneled maximum mean discrepancy loss. We simulated generative modeling of the Bars-and-Stripes dataset and Gaussian mixture distributions using deep quantum circuits. Our experiments show the importance of circuit depth and gradient-based optimization algorithm. The proposed learning algorithm is runnable on near-term quantum device and can exhibit quantum advantages for generative modeling.