Neural Term Structure of Additive Process for Option Pricing

The additive process generalizes the L\'evy process by relaxing its assumption of time-homogeneous increments and hence covers a larger family of stochastic processes. Recent research in option pricing shows that modeling the underlying log price with an additive process has advantages in easier construction of the risk-neural measure, an explicit option pricing formula and characteristic function, and more flexibility to fit the implied volatility surface. Still, the challenge of calibrating an additive model arises from its time-dependent parameterization, for which one has to prescribe parametric functions for the term structure. For this, we propose the neural term structure model to utilize feedforward neural networks to represent the term structure, which alleviates the difficulty of designing parametric functions and thus attenuates the misspecification risk. Numerical studies with S\&P 500 option data are conducted to evaluate the performance of the neural term structure.

NeuralBeta: Estimating Beta Using Deep Learning

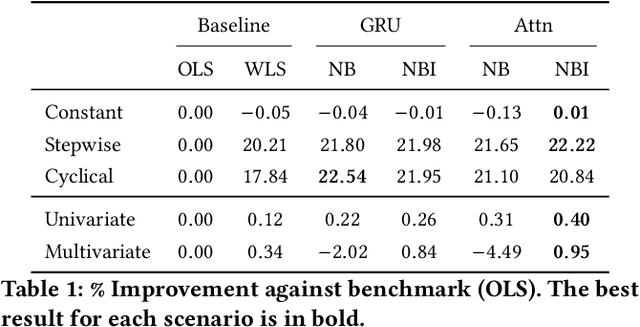
Traditional approaches to estimating beta in finance often involve rigid assumptions and fail to adequately capture beta dynamics, limiting their effectiveness in use cases like hedging. To address these limitations, we have developed a novel method using neural networks called NeuralBeta, which is capable of handling both univariate and multivariate scenarios and tracking the dynamic behavior of beta. To address the issue of interpretability, we introduce a new output layer inspired by regularized weighted linear regression, which provides transparency into the model's decision-making process. We conducted extensive experiments on both synthetic and market data, demonstrating NeuralBeta's superior performance compared to benchmark methods across various scenarios, especially instances where beta is highly time-varying, e.g., during regime shifts in the market. This model not only represents an advancement in the field of beta estimation, but also shows potential for applications in other financial contexts that assume linear relationships.