Efficient optimization-based trajectory planning

This study proposes a unified optimization-based planning framework that addresses the precise and efficient navigation of a controlled object within a constrained region, while contending with obstacles. We focus on handling two collision avoidance problems, i.e., the object not colliding with obstacles and not colliding with boundaries of the constrained region. The object or obstacle is denoted as a union of convex polytopes and ellipsoids, and the constrained region is denoted as an intersection of such convex sets. Using these representations, collision avoidance can be approached by formulating explicit constraints that separate two convex sets, or ensure that a convex set is contained in another convex set, referred to as separating constraints and containing constraints, respectively. We propose to use the hyperplane separation theorem to formulate differentiable separating constraints, and utilize the S-procedure and geometrical methods to formulate smooth containing constraints. We state that compared to the state of the art, the proposed formulations allow a considerable reduction in nonlinear program size and geometry-based initialization in auxiliary variables used to formulate collision avoidance constraints. Finally, the efficacy of the proposed unified planning framework is evaluated in two contexts, autonomous parking in tractor-trailer vehicles and overtaking on curved lanes. The results in both cases exhibit an improved computational performance compared to existing methods.

Efficient collision avoidance for autonomous vehicles in polygonal domains

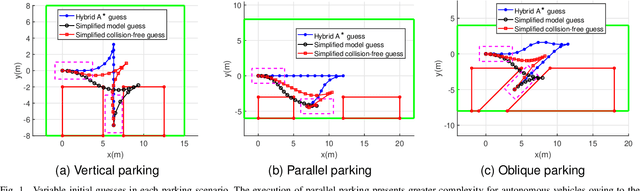
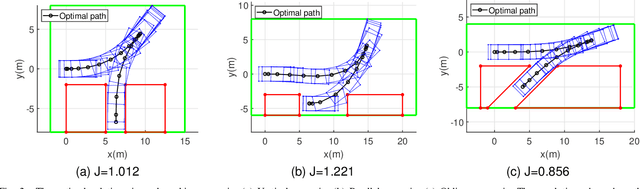
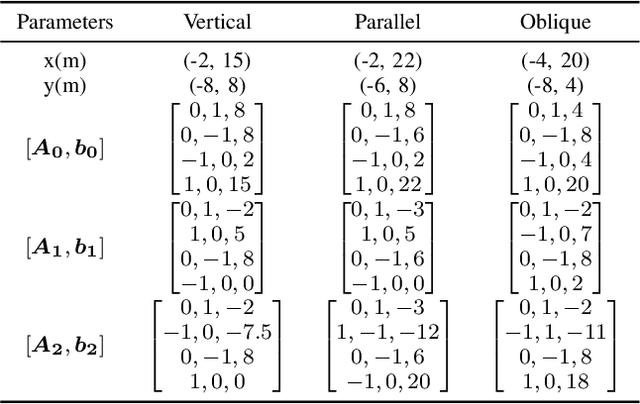
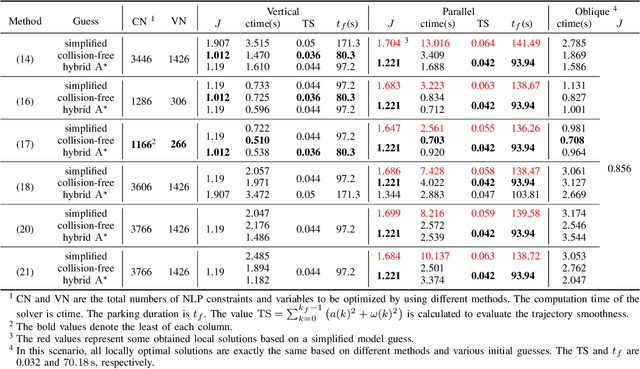
This research focuses on trajectory planning problems for autonomous vehicles utilizing numerical optimal control techniques. The study reformulates the constrained optimization problem into a nonlinear programming problem, incorporating explicit collision avoidance constraints. We present three novel, exact formulations to describe collision constraints. The first formulation is derived from a proposition concerning the separation of a point and a convex set. We prove the separating proposition through De Morgan's laws. Then, leveraging the hyperplane separation theorem we propose two efficient reformulations. Compared with the existing dual formulations and the first formulation, they significantly reduce the number of auxiliary variables to be optimized and inequality constraints within the nonlinear programming problem. Finally, the efficacy of the proposed formulations is demonstrated in the context of typical autonomous parking scenarios compared with state of the art. For generality, we design three initial guesses to assess the computational effort required for convergence to solutions when using the different collision formulations. The results illustrate that the scheme employing De Morgan's laws performs equally well with those utilizing dual formulations, while the other two schemes based on hyperplane separation theorem exhibit the added benefit of requiring lower computational resources.