Jianmei Luo
Hybridized Threshold Clustering for Massive Data
Jul 05, 2019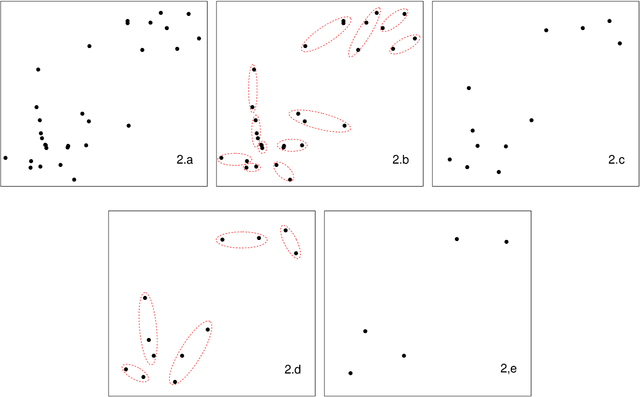
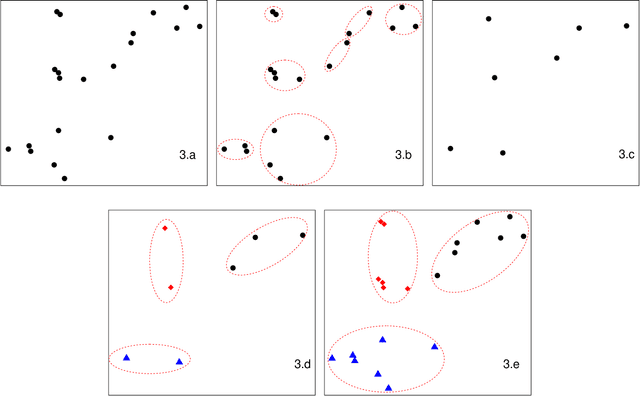
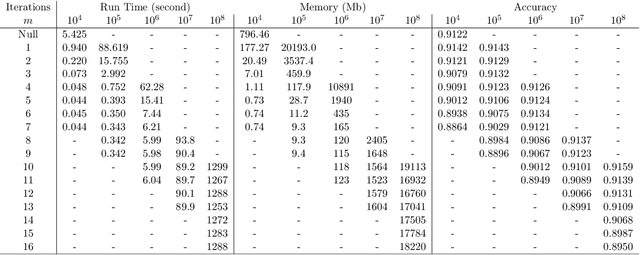
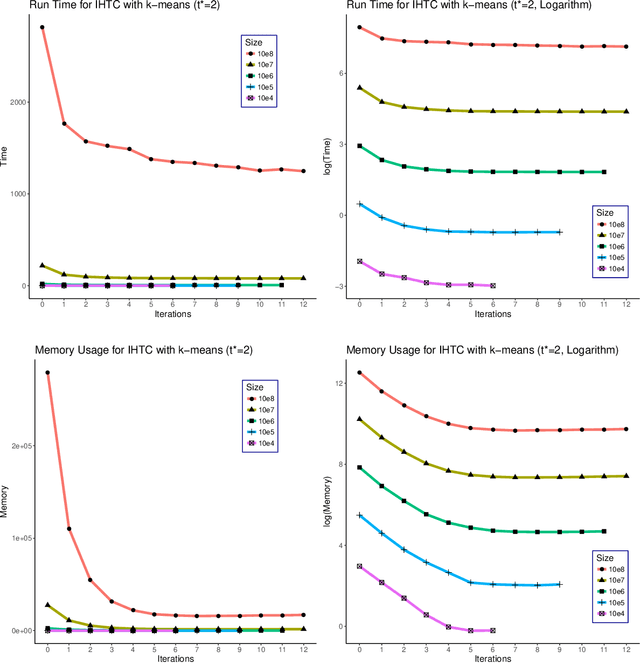
Abstract:As the size $n$ of datasets become massive, many commonly-used clustering algorithms (for example, $k$-means or hierarchical agglomerative clustering (HAC) require prohibitive computational cost and memory. In this paper, we propose a solution to these clustering problems by extending threshold clustering (TC) to problems of instance selection. TC is a recently developed clustering algorithm designed to partition data into many small clusters in linearithmic time (on average). Our proposed clustering method is as follows. First, TC is performed and clusters are reduced into single "prototype" points. Then, TC is applied repeatedly on these prototype points until sufficient data reduction has been obtained. Finally, a more sophisticated clustering algorithm is applied to the reduced prototype points, thereby obtaining a clustering on all $n$ data points. This entire procedure for clustering is called iterative hybridized threshold clustering (IHTC). Through simulation results and by applying our methodology on several real datasets, we show that IHTC combined with $k$-means or HAC substantially reduces the run time and memory usage of the original clustering algorithms while still preserving their performance. Additionally, IHTC helps prevent singular data points from being overfit by clustering algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge