MIRROR: A Multi-Agent Framework with Iterative Adaptive Revision and Hierarchical Retrieval for Optimization Modeling in Operations Research

Operations Research (OR) relies on expert-driven modeling-a slow and fragile process ill-suited to novel scenarios. While large language models (LLMs) can automatically translate natural language into optimization models, existing approaches either rely on costly post-training or employ multi-agent frameworks, yet most still lack reliable collaborative error correction and task-specific retrieval, often leading to incorrect outputs. We propose MIRROR, a fine-tuning-free, end-to-end multi-agent framework that directly translates natural language optimization problems into mathematical models and solver code. MIRROR integrates two core mechanisms: (1) execution-driven iterative adaptive revision for automatic error correction, and (2) hierarchical retrieval to fetch relevant modeling and coding exemplars from a carefully curated exemplar library. Experiments show that MIRROR outperforms existing methods on standard OR benchmarks, with notable results on complex industrial datasets such as IndustryOR and Mamo-ComplexLP. By combining precise external knowledge infusion with systematic error correction, MIRROR provides non-expert users with an efficient and reliable OR modeling solution, overcoming the fundamental limitations of general-purpose LLMs in expert optimization tasks.

TIDE: Tuning-Integrated Dynamic Evolution for LLM-Based Automated Heuristic Design

Although Large Language Models have advanced Automated Heuristic Design, treating algorithm evolution as a monolithic text generation task overlooks the coupling between discrete algorithmic structures and continuous numerical parameters. Consequently, existing methods often discard promising algorithms due to uncalibrated constants and suffer from premature convergence resulting from simple similarity metrics. To address these limitations, we propose TIDE, a Tuning-Integrated Dynamic Evolution framework designed to decouple structural reasoning from parameter optimization. TIDE features a nested architecture where an outer parallel island model utilizes Tree Similarity Edit Distance to drive structural diversity, while an inner loop integrates LLM-based logic generation with a differential mutation operator for parameter tuning. Additionally, a UCB-based scheduler dynamically prioritizes high-yield prompt strategies to optimize resource allocation. Extensive experiments across nine combinatorial optimization problems demonstrate that TIDE discovers heuristics that significantly outperform state-of-the-art baselines in solution quality while achieving improved search efficiency and reduced computational costs.

Multi-Objectivizing Sum-of-the-Parts Combinatorial Optimization Problems by Random Objective Decomposition

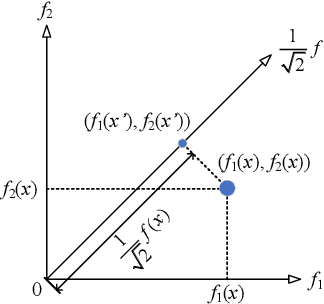
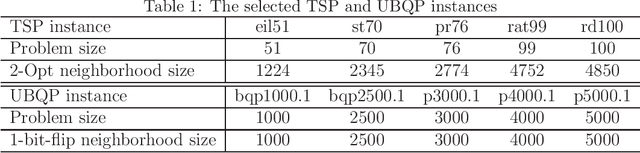
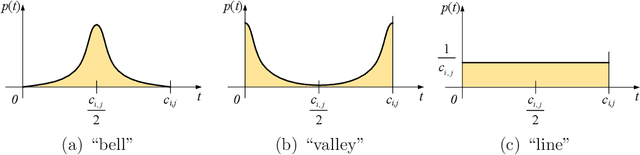
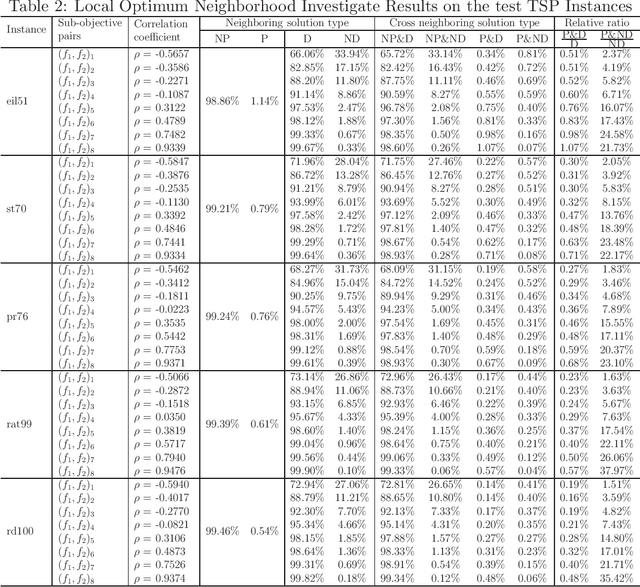
Multi-objectivization is a term used to describe strategies developed for optimizing single-objective problems by multi-objective algorithms. This paper focuses on the multi-objectivization of the sum-of-the-parts Combinatorial Optimization Problems (COPs), which include the Traveling Salesman Problem (TSP), the Unconstrained Binary Quadratic Programming (UBQP) and other well-known COPs. For a sum-of-the-parts COP, we propose to decompose its original objective into two sub-objectives with controllable correlation. Based on the decomposition method, two new multi-objectivization techniques called Non-Dominance Search (NDS) and Non-Dominance Exploitation (NDE) are developed, respectively. NDS is combined with the Iterated Local Search (ILS) metaheuristic (with fixed neighborhood structure), while NDE is embedded within the Iterated Lin-Kernighan (ILK) metaheuristic (with varied neighborhood structure). The resultant metaheuristics are called ILS+NDS and ILK+NDE, respectively. Empirical studies on some TSP and UBQP instances show that with appropriate correlation between the sub-objectives, there are more chances to escape from local optima when new starting solution is selected from the non-dominated solutions defined by the decomposed sub-objectives. Experimental results also show that ILS+NDS and ILK+NDE both significantly outperform their counterparts on most of the test instances.

EB-GLS: An Improved Guided Local Search Based on the Big Valley Structure

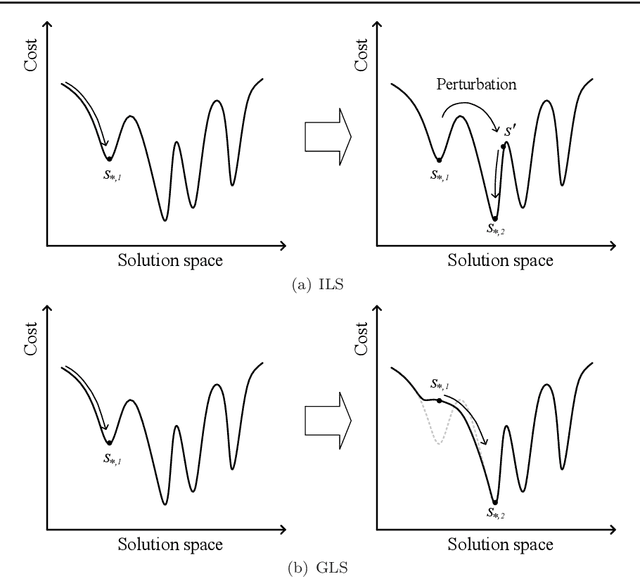
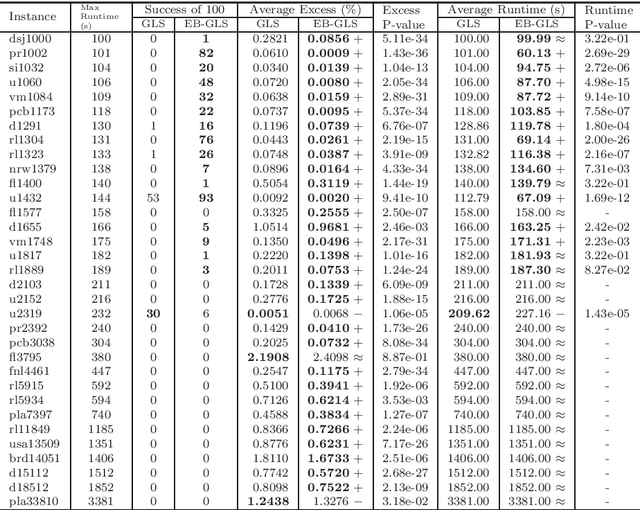
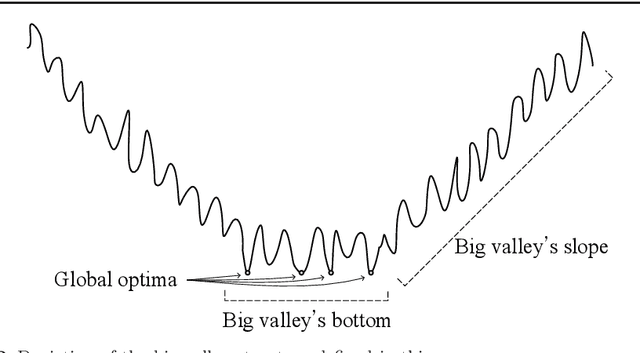
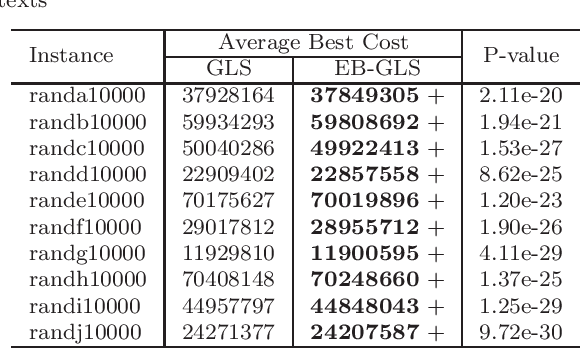
Local search is a basic building block in memetic algorithms. Guided Local Search (GLS) can improve the efficiency of local search. By changing the guide function, GLS guides a local search to escape from locally optimal solutions and find better solutions. The key component of GLS is its penalizing mechanism which determines which feature is selected to penalize when the search is trapped in a locally optimal solution. The original GLS penalizing mechanism only makes use of the cost and the current penalty value of each feature. It is well known that many combinatorial optimization problems have a big valley structure, i.e., the better a solution is, the more the chance it is closer to a globally optimal solution. This paper proposes to use big valley structure assumption to improve the GLS penalizing mechanism. An improved GLS algorithm called Elite Biased GLS (EB-GLS) is proposed. EB-GLS records and maintains an elite solution as an estimate of the globally optimal solutions, and reduces the chance of penalizing the features in this solution. We have systematically tested the proposed algorithm on the symmetric traveling salesman problem. Experimental results show that EB-GLS is significantly better than GLS.