Multi-Objectivizing Sum-of-the-Parts Combinatorial Optimization Problems by Random Objective Decomposition

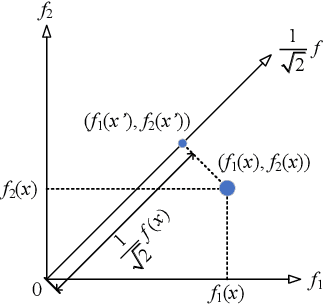
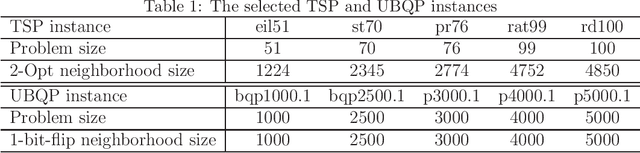
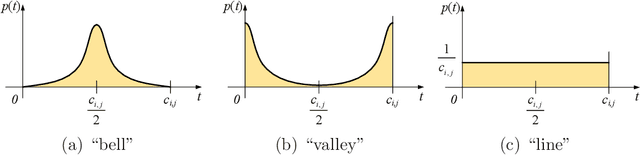
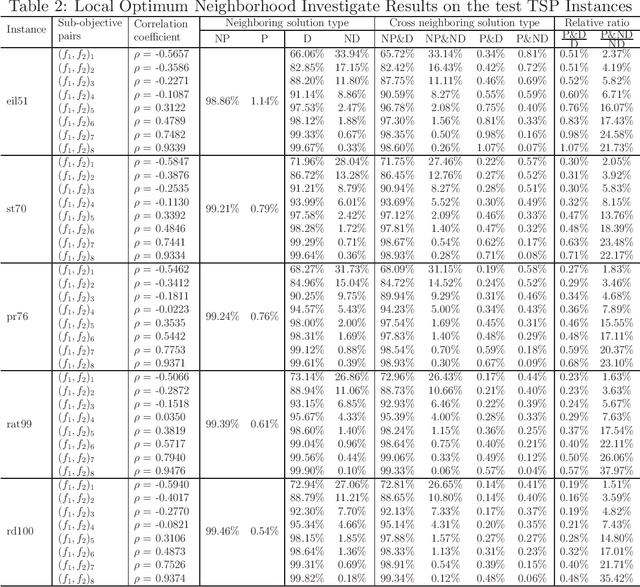
Multi-objectivization is a term used to describe strategies developed for optimizing single-objective problems by multi-objective algorithms. This paper focuses on the multi-objectivization of the sum-of-the-parts Combinatorial Optimization Problems (COPs), which include the Traveling Salesman Problem (TSP), the Unconstrained Binary Quadratic Programming (UBQP) and other well-known COPs. For a sum-of-the-parts COP, we propose to decompose its original objective into two sub-objectives with controllable correlation. Based on the decomposition method, two new multi-objectivization techniques called Non-Dominance Search (NDS) and Non-Dominance Exploitation (NDE) are developed, respectively. NDS is combined with the Iterated Local Search (ILS) metaheuristic (with fixed neighborhood structure), while NDE is embedded within the Iterated Lin-Kernighan (ILK) metaheuristic (with varied neighborhood structure). The resultant metaheuristics are called ILS+NDS and ILK+NDE, respectively. Empirical studies on some TSP and UBQP instances show that with appropriate correlation between the sub-objectives, there are more chances to escape from local optima when new starting solution is selected from the non-dominated solutions defined by the decomposed sub-objectives. Experimental results also show that ILS+NDS and ILK+NDE both significantly outperform their counterparts on most of the test instances.