Mistake-bounded online learning with operation caps

We investigate the mistake-bound model of online learning with caps on the number of arithmetic operations per round. We prove general bounds on the minimum number of arithmetic operations per round that are necessary to learn an arbitrary family of functions with finitely many mistakes. We solve a problem on agnostic mistake-bounded online learning with bandit feedback from (Filmus et al, 2024) and (Geneson \& Tang, 2024). We also extend this result to the setting of operation caps.

Bounds on the price of feedback for mistake-bounded online learning

We improve several worst-case bounds for various online learning scenarios from (Auer and Long, Machine Learning, 1999). In particular, we sharpen an upper bound for delayed ambiguous reinforcement learning by a factor of 2 and an upper bound for learning compositions of families of functions by a factor of 2.41. We also improve a lower bound from the same paper for learning compositions of $k$ families of functions by a factor of $\Theta(\ln{k})$, matching the upper bound up to a constant factor. In addition, we solve a problem from (Long, Theoretical Computer Science, 2020) on the price of bandit feedback with respect to standard feedback for multiclass learning, and we improve an upper bound from (Feng et al., Theoretical Computer Science, 2023) on the price of $r$-input delayed ambiguous reinforcement learning by a factor of $r$, matching a lower bound from the same paper up to the leading term.

Online Learning of Smooth Functions

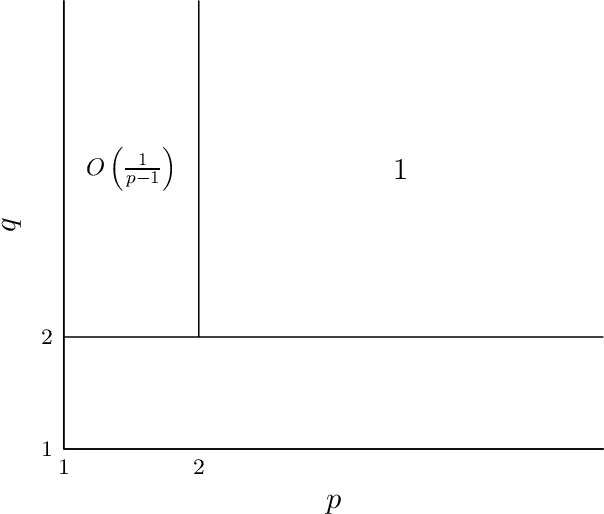
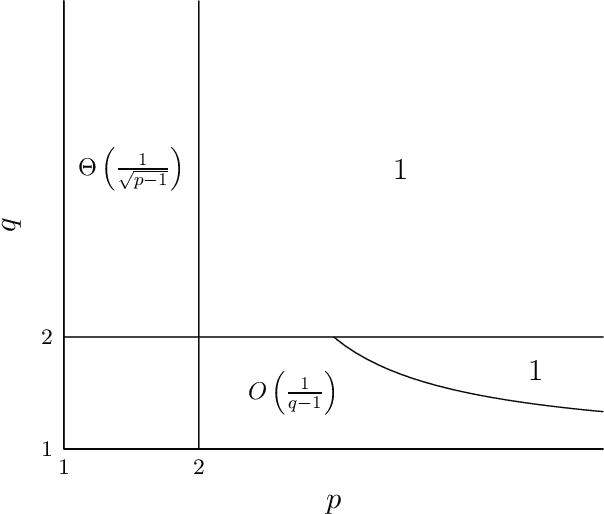
In this paper, we study the online learning of real-valued functions where the hidden function is known to have certain smoothness properties. Specifically, for $q \ge 1$, let $\mathcal F_q$ be the class of absolutely continuous functions $f: [0,1] \to \mathbb R$ such that $\|f'\|_q \le 1$. For $q \ge 1$ and $d \in \mathbb Z^+$, let $\mathcal F_{q,d}$ be the class of functions $f: [0,1]^d \to \mathbb R$ such that any function $g: [0,1] \to \mathbb R$ formed by fixing all but one parameter of $f$ is in $\mathcal F_q$. For any class of real-valued functions $\mathcal F$ and $p>0$, let $\text{opt}_p(\mathcal F)$ be the best upper bound on the sum of $p^{\text{th}}$ powers of absolute prediction errors that a learner can guarantee in the worst case. In the single-variable setup, we find new bounds for $\text{opt}_p(\mathcal F_q)$ that are sharp up to a constant factor. We show for all $\varepsilon \in (0, 1)$ that $\text{opt}_{1+\varepsilon}(\mathcal{F}_{\infty}) = \Theta(\varepsilon^{-\frac{1}{2}})$ and $\text{opt}_{1+\varepsilon}(\mathcal{F}_q) = \Theta(\varepsilon^{-\frac{1}{2}})$ for all $q \ge 2$. We also show for $\varepsilon \in (0,1)$ that $\text{opt}_2(\mathcal F_{1+\varepsilon})=\Theta(\varepsilon^{-1})$. In addition, we obtain new exact results by proving that $\text{opt}_p(\mathcal F_q)=1$ for $q \in (1,2)$ and $p \ge 2+\frac{1}{q-1}$. In the multi-variable setup, we establish inequalities relating $\text{opt}_p(\mathcal F_{q,d})$ to $\text{opt}_p(\mathcal F_q)$ and show that $\text{opt}_p(\mathcal F_{\infty,d})$ is infinite when $p<d$ and finite when $p>d$. We also obtain sharp bounds on learning $\mathcal F_{\infty,d}$ for $p < d$ when the number of trials is bounded.

Sharp bounds on the price of bandit feedback for several models of mistake-bounded online learning

We determine sharp bounds on the price of bandit feedback for several variants of the mistake-bound model. The first part of the paper presents bounds on the $r$-input weak reinforcement model and the $r$-input delayed, ambiguous reinforcement model. In both models, the adversary gives $r$ inputs in each round and only indicates a correct answer if all $r$ guesses are correct. The only difference between the two models is that in the delayed, ambiguous model, the learner must answer each input before receiving the next input of the round, while the learner receives all $r$ inputs at once in the weak reinforcement model. In the second part of the paper, we introduce models for online learning with permutation patterns, in which a learner attempts to learn a permutation from a set of permutations by guessing statistics related to sub-permutations. For these permutation models, we prove sharp bounds on the price of bandit feedback.

Sharper bounds for online learning of smooth functions of a single variable

We investigate the generalization of the mistake-bound model to continuous real-valued single variable functions. Let $\mathcal{F}_q$ be the class of absolutely continuous functions $f: [0, 1] \rightarrow \mathbb{R}$ with $||f'||_q \le 1$, and define $opt_p(\mathcal{F}_q)$ as the best possible bound on the worst-case sum of the $p^{th}$ powers of the absolute prediction errors over any number of trials. Kimber and Long (Theoretical Computer Science, 1995) proved for $q \ge 2$ that $opt_p(\mathcal{F}_q) = 1$ when $p \ge 2$ and $opt_p(\mathcal{F}_q) = \infty$ when $p = 1$. For $1 < p < 2$ with $p = 1+\epsilon$, the only known bound was $opt_p(\mathcal{F}_{q}) = O(\epsilon^{-1})$ from the same paper. We show for all $\epsilon \in (0, 1)$ and $q \ge 2$ that $opt_{1+\epsilon}(\mathcal{F}_q) = \Theta(\epsilon^{-\frac{1}{2}})$, where the constants in the bound do not depend on $q$. We also show that $opt_{1+\epsilon}(\mathcal{F}_{\infty}) = \Theta(\epsilon^{-\frac{1}{2}})$.

A note on the price of bandit feedback for mistake-bounded online learning

The standard model and the bandit model are two generalizations of the mistake-bound model to online multiclass classification. In both models the learner guesses a classification in each round, but in the standard model the learner recieves the correct classification after each guess, while in the bandit model the learner is only told whether or not their guess is correct in each round. For any set $F$ of multiclass classifiers, define $opt_{std}(F)$ and $opt_{bandit}(F)$ to be the optimal worst-case number of prediction mistakes in the standard and bandit models respectively. Long (Theoretical Computer Science, 2020) claimed that for all $M > 2$ and infinitely many $k$, there exists a set $F$ of functions from a set $X$ to a set $Y$ of size $k$ such that $opt_{std}(F) = M$ and $opt_{bandit}(F) \ge (1 - o(1))(|Y|\ln{|Y|})opt_{std}(F)$. The proof of this result depended on the following lemma, which is false e.g. for all prime $p \ge 5$, $s = \mathbf{1}$ (the all $1$ vector), $t = \mathbf{2}$ (the all $2$ vector), and all $z$. Lemma: Fix $n \ge 2$ and prime $p$, and let $u$ be chosen uniformly at random from $\left\{0, \dots, p-1\right\}^n$. For any $s, t \in \left\{1, \dots, p-1\right\}^n$ with $s \neq t$ and for any $z \in \left\{0, \dots, p-1\right\}$, we have $\Pr(t \cdot u = z \mod p \text{ } | \text{ } s \cdot u = z \mod p) = \frac{1}{p}$. We show that this lemma is false precisely when $s$ and $t$ are multiples of each other mod $p$. Then using a new lemma, we fix Long's proof.