Clustering categorical data via ensembling dissimilarity matrices

We present a technique for clustering categorical data by generating many dissimilarity matrices and averaging over them. We begin by demonstrating our technique on low dimensional categorical data and comparing it to several other techniques that have been proposed. Then we give conditions under which our method should yield good results in general. Our method extends to high dimensional categorical data of equal lengths by ensembling over many choices of explanatory variables. In this context we compare our method with two other methods. Finally, we extend our method to high dimensional categorical data vectors of unequal length by using alignment techniques to equalize the lengths. We give examples to show that our method continues to provide good results, in particular, better in the context of genome sequences than clusterings suggested by phylogenetic trees.

A General Hybrid Clustering Technique

Here, we propose a clustering technique for general clustering problems including those that have non-convex clusters. For a given desired number of clusters $K$, we use three stages to find a clustering. The first stage uses a hybrid clustering technique to produce a series of clusterings of various sizes (randomly selected). They key steps are to find a $K$-means clustering using $K_\ell$ clusters where $K_\ell \gg K$ and then joins these small clusters by using single linkage clustering. The second stage stabilizes the result of stage one by reclustering via the `membership matrix' under Hamming distance to generate a dendrogram. The third stage is to cut the dendrogram to get $K^*$ clusters where $K^* \geq K$ and then prune back to $K$ to give a final clustering. A variant on our technique also gives a reasonable estimate for $K_T$, the true number of clusters. We provide a series of arguments to justify the steps in the stages of our methods and we provide numerous examples involving real and simulated data to compare our technique with other related techniques.

An ensemble approach to improved prediction from multitype data

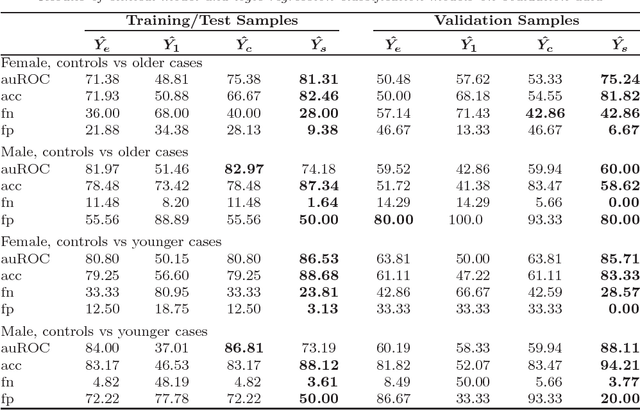
We have developed a strategy for the analysis of newly available binary data to improve outcome predictions based on existing data (binary or non-binary). Our strategy involves two modeling approaches for the newly available data, one combining binary covariate selection via LASSO with logistic regression and one based on logic trees. The results of these models are then compared to the results of a model based on existing data with the objective of combining model results to achieve the most accurate predictions. The combination of model predictions is aided by the use of support vector machines to identify subspaces of the covariate space in which specific models lead to successful predictions. We demonstrate our approach in the analysis of single nucleotide polymorphism (SNP) data and traditional clinical risk factors for the prediction of coronary heart disease.