Rank-Preference Consistency as the Appropriate Metric for Recommender Systems

In this paper we argue that conventional unitary-invariant measures of recommender system (RS) performance based on measuring differences between predicted ratings and actual user ratings fail to assess fundamental RS properties. More specifically, posing the optimization problem as one of predicting exact user ratings provides only an indirect suboptimal approximation for what RS applications typically need, which is an ability to accurately predict user preferences. We argue that scalar measures such as RMSE and MAE with respect to differences between actual and predicted ratings are only proxies for measuring RS ability to accurately estimate user preferences. We propose what we consider to be a measure that is more fundamentally appropriate for assessing RS performance, rank-preference consistency, which simply counts the number of prediction pairs that are inconsistent with the user's expressed product preferences. For example, if an RS predicts the user will prefer product A over product B, but the user's withheld ratings indicate s/he prefers product B over A, then rank-preference consistency has been violated. Our test results conclusively demonstrate that methods tailored to optimize arbitrary measures such as RMSE are not generally effective at accurately predicting user preferences. Thus, we conclude that conventional methods used for assessing RS performance are arbitrary and misleading.

Partial Proof of a Conjecture with Implications for Spectral Majorization

In this paper we report on new results relating to a conjecture regarding properties of $n\times n$, $n\leq 6$, positive definite matrices. The conjecture has been proven for $n\leq 4$ using computer-assisted sum of squares (SoS) methods for proving polynomial nonnegativity. Based on these proven cases, we report on the recent identification of a new family of matrices with the property that their diagonals majorize their spectrum. We then present new results showing that this family can extended via Kronecker composition to $n>6$ while retaining the special majorization property. We conclude with general considerations on the future of computer-assisted and AI-based proofs.

Choosing the Correct Generalized Inverse for the Numerical Solution of the Inverse Kinematics of Incommensurate Robotic Manipulators

Numerical methods for Inverse Kinematics (IK) employ iterative, linear approximations of the IK until the end-effector is brought from its initial pose to the desired final pose. These methods require the computation of the Jacobian of the Forward Kinematics (FK) and its inverse in the linear approximation of the IK. Despite all the successful implementations reported in the literature, Jacobian-based IK methods can still fail to preserve certain useful properties if an improper matrix inverse, e.g. Moore-Penrose (MP), is employed for incommensurate robotic systems. In this paper, we propose a systematic, robust and accurate numerical solution for the IK problem using the Mixed (MX) Generalized Inverse (GI) applied to any type of Jacobians (e.g., analytical, numerical or geometric) derived for any commensurate and incommensurate robot. This approach is robust to whether the system is under-determined (less than 6 DoF) or over-determined (more than 6 DoF). We investigate six robotics manipulators with various Degrees of Freedom (DoF) to demonstrate that commonly used GI's fail to guarantee the same system behaviors when the units are varied for incommensurate robotics manipulators. In addition, we evaluate the proposed methodology as a global IK solver and compare against well-known IK methods for redundant manipulators. Based on the experimental results, we conclude that the right choice of GI is crucial in preserving certain properties of the system (i.e. unit-consistency).

Achieving Unit-Consistent Pseudo-Inverse-based Path-Planning for Redundant Incommensurate Robotic Manipulators

In this paper, we review and compare several velocity-level and acceleration-level Pseudo-Inverse-based Path Planning (PPP) and Pseudo-Inverse-based Repetitive Motion Planning (PRMP) schemes based on the kinematic model of robotic manipulators. We show that without unit consistency in the pseudo-inverse computation, path planning of incommensurate robotic manipulators will fail. Also, we investigated the robustness and noise tolerance of six PPP and PRMP schemes in the literature against various noise types (i.e. zero, constant, time-varying and random noises). We compared the simulated results using two redundant robotic manipulators: a 3DoF (2RP), and a 7DoF (2RP4R). These experimental results demonstrate that the improper Generalized Inverse (GI) with arbitrary selection of unit and/or in the presence of noise can lead to unexpected behavior of the robot, while producing wrong instantaneous outputs in the task space, which results in distortions and/or failures in the execution of the planned path. Finally, we propose and demonstrate the efficacy of the Mixed Inverse (MX) as the proper GI to achieve unit-consistency in path planning.

An Admissible Shift-Consistent Method for Recommender Systems

In this paper, we propose a new constraint, called shift-consistency, for solving matrix/tensor completion problems in the context of recommender systems. Our method provably guarantees several key mathematical properties: (1) satisfies a recently established admissibility criterion for recommender systems; (2) satisfies a definition of fairness that eliminates a specific class of potential opportunities for users to maliciously influence system recommendations; and (3) offers robustness by exploiting provable uniqueness of missing-value imputation. We provide a rigorous mathematical description of the method, including its generalization from matrix to tensor form to permit representation and exploitation of complex structural relationships among sets of user and product attributes. We argue that our analysis suggests a structured means for defining latent-space projections that can permit provable performance properties to be established for machine learning methods.

Imposing Consistency Properties on Blackbox Systems with Applications to SVD-Based Recommender Systems

In this paper we discuss pre- and post-processing methods to induce desired consistency and/or invariance properties in blackbox systems, e.g., AI-based. We demonstrate our approach in the context of blackbox SVD-based matrix-completion methods commonly used in recommender system (RS) applications. We provide empirical results showing that enforcement of unit-consistency and shift-consistency, which have provable RS-relevant properties relating to robustness and fairness, also lead to improved performance according to generic RMSE and MAE performance metrics, irrespective of the initial chosen hyperparameter.

Metric Search for Rank List Compatibility Matching with Applications

As online dating has become more popular in the past few years, an efficient and effective algorithm to match users is needed. In this project, we proposed a new dating matching algorithm that uses Kendall-Tau distance to measure the similarity between users based on their ranking for items in a list. (e.g., their favourite sports, music, etc.) To increase the performance of the search process, we applied a tree-based searching structure, Cascading Metric Tree (CMT), on this metric. The tree is built on ranked lists from all the users; when a query target and a radius are provided, our algorithm can return users within the radius of the target. We tested the scaling of this searching method on a synthetic dataset by varying list length, population size, and query radius. We observed that the algorithm is able to query the best matching people for the user in a practical time, given reasonable parameters. We also provided potential future improvements that can be made to this algorithm based on the limitations. Finally, we offered more use cases of this search structure on Kendall-Tau distance and new insight into real-world applications of distance search structures.

A Simple and Scalable Tensor Completion Algorithm via Latent Invariant Constraint for Recommendation System

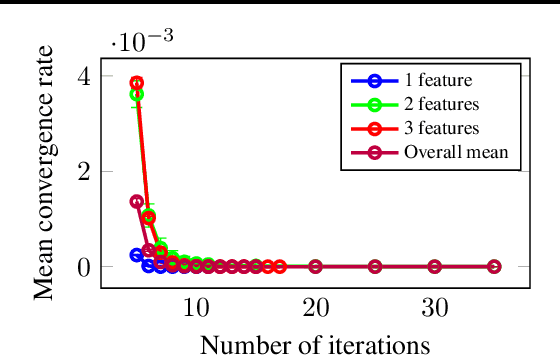
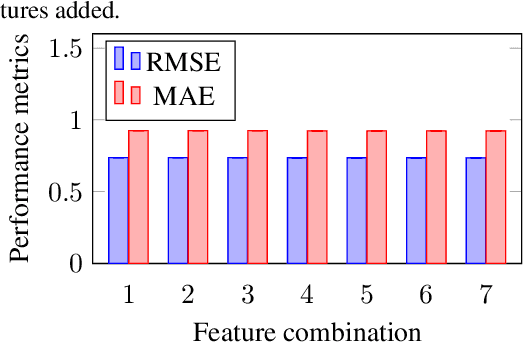
In this paper we provide a latent-variable formulation and solution to the recommender system (RS) problem in terms of a fundamental property that any reasonable solution should be expected to satisfy. Specifically, we examine a novel tensor completion method to efficiently and accurately learn parameters of a model for the unobservable personal preferences that underly user ratings. By regularizing the tensor decomposition with a single latent invariant, we achieve three properties for a reliable recommender system: (1) uniqueness of the tensor completion result with minimal assumptions, (2) unit consistency that is independent of arbitrary preferences of users, and (3) a consensus ordering guarantee that provides consistent ranking between observed and unobserved rating scores. Our algorithm leads to a simple and elegant recommendation framework that has linear computational complexity and with no hyperparameter tuning. We provide empirical results demonstrating that the approach significantly outperforms current state-of-the-art methods.

A Unit-Consistent Tensor Completion with Applications in Recommender Systems

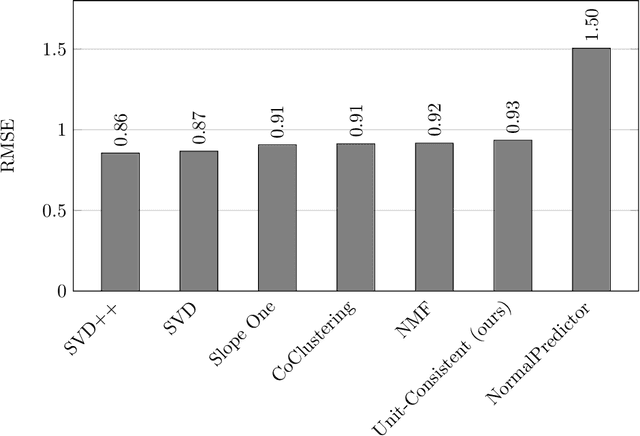
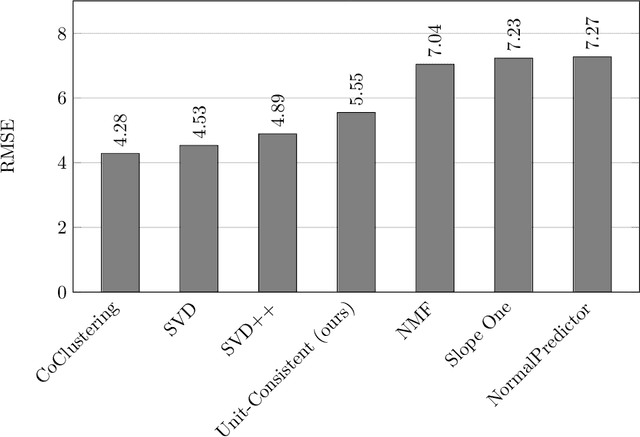
In this paper we introduce a new consistency-based approach for defining and solving nonnegative/positive matrix and tensor completion problems. The novelty of the framework is that instead of artificially making the problem well-posed in the form of an application-arbitrary optimization problem, e.g., minimizing a bulk structural measure such as rank or norm, we show that a single property/constraint - preserving unit-scale consistency - guarantees both existence of a solution and, under relatively weak support assumptions, uniqueness. The framework and solution algorithms also generalize directly to tensors of arbitrary dimension while maintaining computational complexity that is linear in problem size for fixed dimension d. In the context of recommender system (RS) applications, we prove that two reasonable properties that should be expected to hold for any solution to the RS problem are sufficient to permit uniqueness guarantees to be established within our framework. This is remarkable because it obviates the need for heuristic-based statistical or AI methods despite what appear to be distinctly human/subjective variables at the heart of the problem. Key theoretical contributions include a general unit-consistent tensor-completion framework with proofs of its properties, including algorithms with optimal runtime complexity, e.g., O(1) term-completion with preprocessing complexity that is linear in the number of known terms of the matrix/tensor.

Covapixels

We propose and discuss the summarization of superpixel-type image tiles/patches using mean and covariance information. We refer to the resulting objects as covapixels.