Consistent Regression using Data-Dependent Coverings

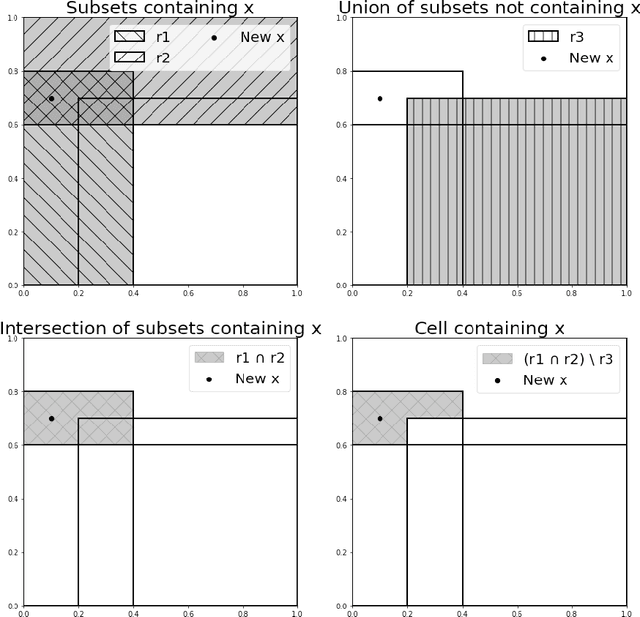
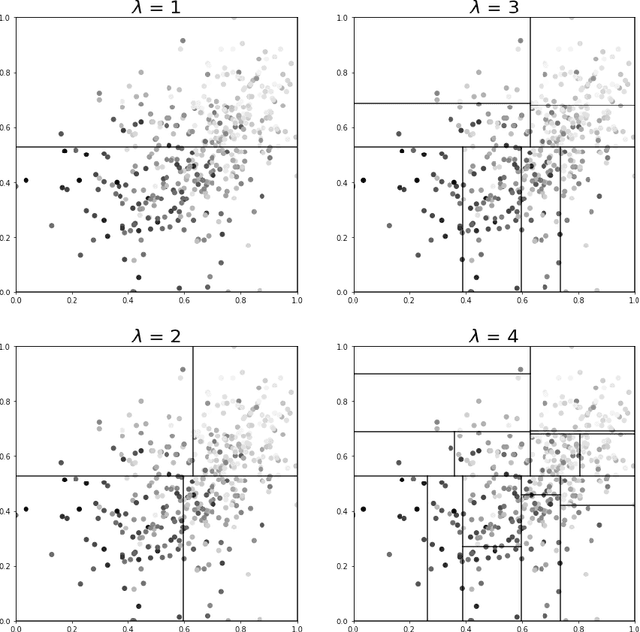
In this paper, we introduce a novel method to generate interpretable regression function estimators. The idea is based on called data-dependent coverings. The aim is to extract from the data a covering of the feature space instead of a partition. The estimator predicts the empirical conditional expectation over the cells of the partitions generated from the coverings. Thus, such estimator has the same form as those issued from data-dependent partitioning algorithms. We give sufficient conditions to ensure the consistency, avoiding the sufficient condition of shrinkage of the cells that appears in the former literature. Doing so, we reduce the number of covering elements. We show that such coverings are interpretable and each element of the covering is tagged as significant or insignificant. The proof of the consistency is based on a control of the error of the empirical estimation of conditional expectations which is interesting on its own.

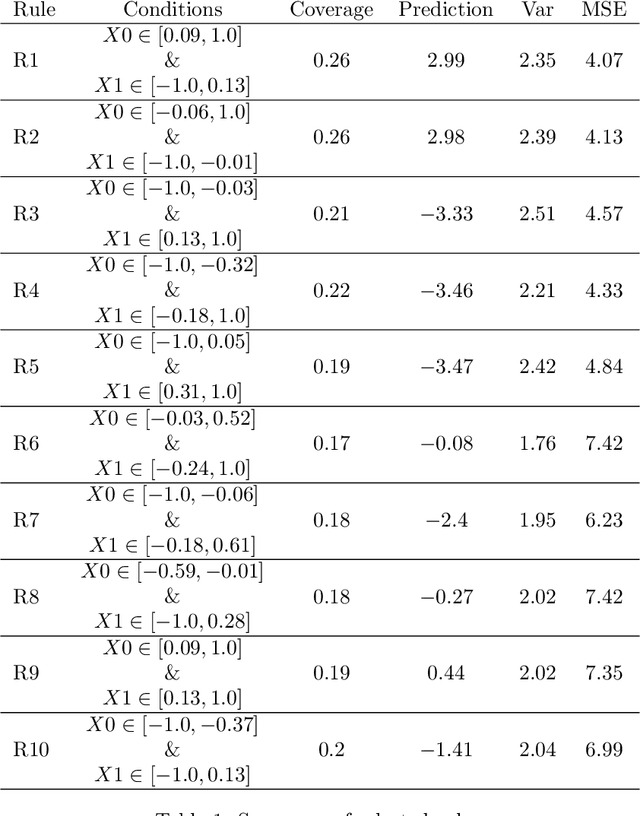
Rule Induction Partitioning Estimator

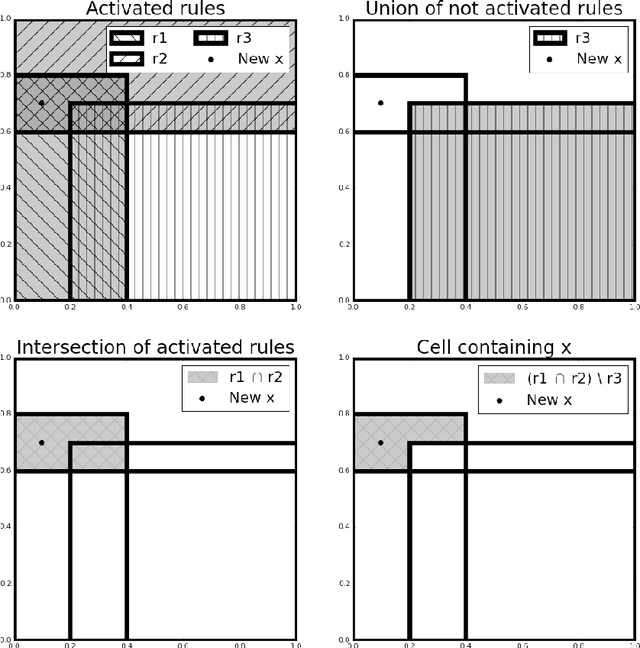
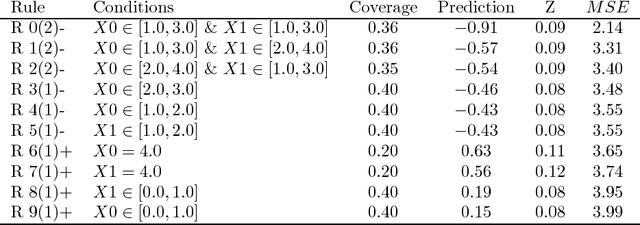
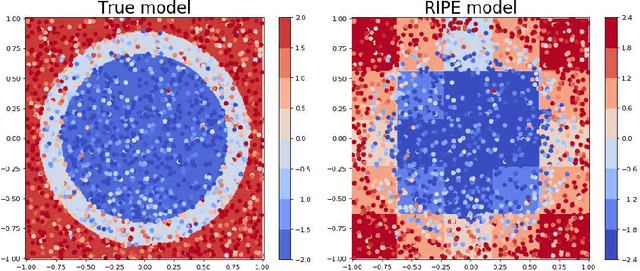
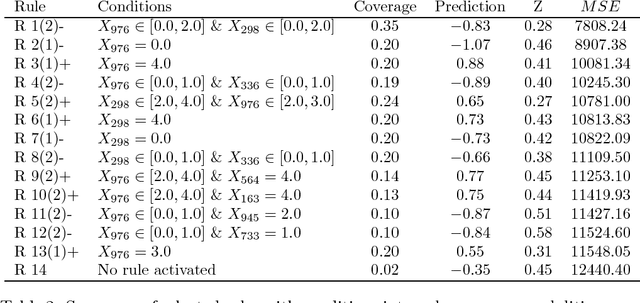
RIPE is a novel deterministic and easily understandable prediction algorithm developed for continuous and discrete ordered data. It infers a model, from a sample, to predict and to explain a real variable $Y$ given an input variable $X \in \mathcal X$ (features). The algorithm extracts a sparse set of hyperrectangles $\mathbf r \subset \mathcal X$, which can be thought of as rules of the form If-Then. This set is then turned into a partition of the features space $\mathcal X$ of which each cell is explained as a list of rules with satisfied their If conditions. The process of RIPE is illustrated on simulated datasets and its efficiency compared with that of other usual algorithms.