Heterogeneity in Neuronal Calcium Spike Trains based on Empirical Distance

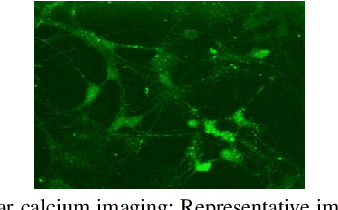
Statistical similarities between neuronal spike trains could reveal significant information on complex underlying processing. In general, the similarity between synchronous spike trains is somewhat easy to identify. However, the similar patterns also potentially appear in an asynchronous manner. However, existing methods for their identification tend to converge slowly, and cannot be applied to short sequences. In response, we propose Hellinger distance measure based on empirical probabilities, which we show to be as accurate as existing techniques, yet faster to converge for synthetic as well as experimental spike trains. Further, we cluster pairs of neuronal spike trains based on statistical similarities and found two non-overlapping classes, which could indicate functional similarities in neurons. Significantly, our technique detected functional heterogeneity in pairs of neuronal responses with the same performance as existing techniques, while exhibiting faster convergence. We expect the proposed method to facilitate large-scale studies of functional clustering, especially involving short sequences, which would in turn identify signatures of various diseases in terms of clustering patterns.

Information Content in Neuronal Calcium Spike Trains: Entropy Rate Estimation based on Empirical Probabilities

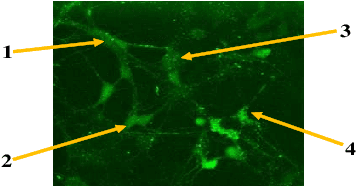
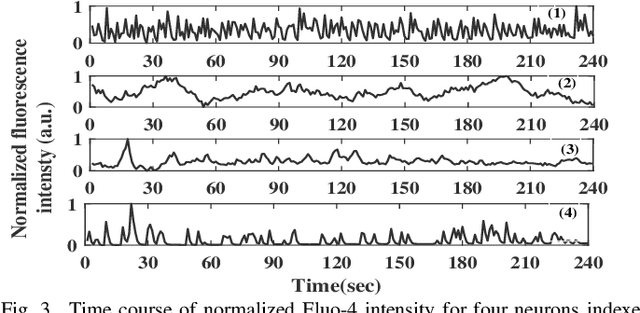
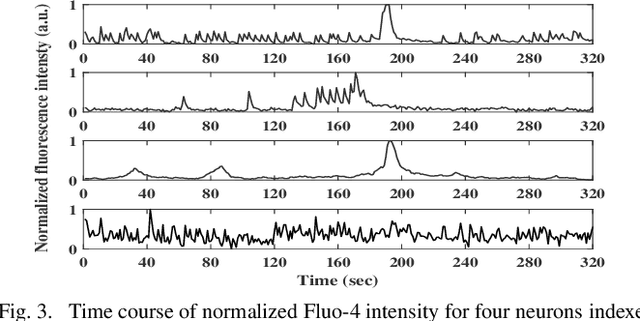
Quantification of information content and its temporal variation in intracellular calcium spike trains in neurons helps one understand functions such as memory, learning, and cognition. Such quantification could also reveal pathological signaling perturbation that potentially leads to devastating neurodegenerative conditions including Parkinson's, Alzheimer's, and Huntington's diseases. Accordingly, estimation of entropy rate, an information-theoretic measure of information content, assumes primary significance. However, such estimation in the present context is challenging because, while entropy rate is traditionally defined asymptotically for long blocks under the assumption of stationarity, neurons are known to encode information in short intervals and the associated spike trains often exhibit nonstationarity. Against this backdrop, we propose an entropy rate estimator based on empirical probabilities that operates within windows, short enough to ensure approximate stationarity. Specifically, our estimator, parameterized by the length of encoding contexts, attempts to model the underlying memory structures in neuronal spike trains. In an example Markov process, we compared the performance of the proposed method with that of versions of the Lempel-Ziv algorithm as well as with that of a certain stationary distribution method and found the former to exhibit higher accuracy levels and faster convergence. Also, in experimentally recorded calcium responses of four hippocampal neurons, the proposed method showed faster convergence. Significantly, our technique detected structural heterogeneity in the underlying process memory in the responses of the aforementioned neurons. We believe that the proposed method facilitates large-scale studies of such heterogeneity, which could in turn identify signatures of various diseases in terms of entropy rate estimates.