Information Content in Neuronal Calcium Spike Trains: Entropy Rate Estimation based on Empirical Probabilities
Paper and Code
Feb 01, 2021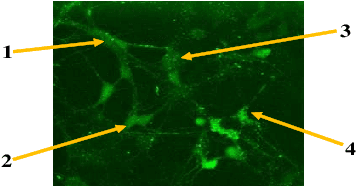

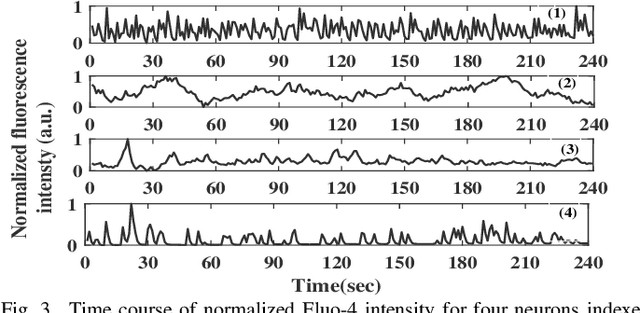

Quantification of information content and its temporal variation in intracellular calcium spike trains in neurons helps one understand functions such as memory, learning, and cognition. Such quantification could also reveal pathological signaling perturbation that potentially leads to devastating neurodegenerative conditions including Parkinson's, Alzheimer's, and Huntington's diseases. Accordingly, estimation of entropy rate, an information-theoretic measure of information content, assumes primary significance. However, such estimation in the present context is challenging because, while entropy rate is traditionally defined asymptotically for long blocks under the assumption of stationarity, neurons are known to encode information in short intervals and the associated spike trains often exhibit nonstationarity. Against this backdrop, we propose an entropy rate estimator based on empirical probabilities that operates within windows, short enough to ensure approximate stationarity. Specifically, our estimator, parameterized by the length of encoding contexts, attempts to model the underlying memory structures in neuronal spike trains. In an example Markov process, we compared the performance of the proposed method with that of versions of the Lempel-Ziv algorithm as well as with that of a certain stationary distribution method and found the former to exhibit higher accuracy levels and faster convergence. Also, in experimentally recorded calcium responses of four hippocampal neurons, the proposed method showed faster convergence. Significantly, our technique detected structural heterogeneity in the underlying process memory in the responses of the aforementioned neurons. We believe that the proposed method facilitates large-scale studies of such heterogeneity, which could in turn identify signatures of various diseases in terms of entropy rate estimates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge