A Differentiable Signed Distance Representation for Continuous Collision Avoidance in Optimization-Based Motion Planning

This paper proposes a new set of conditions for exactly representing collision avoidance constraints within optimization-based motion planning algorithms. The conditions are continuously differentiable and therefore suitable for use with standard nonlinear optimization solvers. The method represents convex shapes using a support function representation and is therefore quite general. For collision avoidance involving polyhedral or ellipsoidal shapes, the proposed method introduces fewer variables and constraints than existing approaches. Additionally the proposed method can be used to rigorously ensure continuous collision avoidance as the vehicle transitions between the discrete poses determined by the motion planning algorithm. Numerical examples demonstrate how this can be used to prevent problems of corner cutting and passing through obstacles which can occur when collision avoidance is only enforced at discrete time steps.

Closed-Form Minkowski Sum Approximations for Efficient Optimization-Based Collision Avoidance

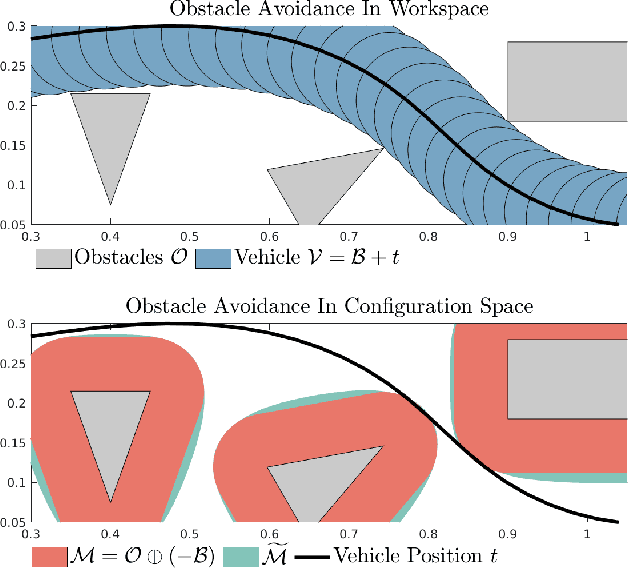
Motion planning methods for autonomous systems based on nonlinear programming offer great flexibility in incorporating various dynamics, objectives, and constraints. One limitation of such tools is the difficulty of efficiently representing obstacle avoidance conditions for non-trivial shapes. For example, it is possible to define collision avoidance constraints suitable for nonlinear programming solvers in the canonical setting of a circular robot navigating around M convex polytopes over N time steps. However, it requires introducing (2+L)MN additional constraints and LMN additional variables, with L being the number of halfplanes per polytope, leading to larger nonlinear programs with slower and less reliable solving time. In this paper, we overcome this issue by building closed-form representations of the collision avoidance conditions by outer-approximating the Minkowski sum conditions for collision. Our solution requires only MN constraints (and no additional variables), leading to a smaller nonlinear program. On motion planning problems for an autonomous car and quadcopter in cluttered environments, we achieve speedups of 4.8x and 8.7x respectively with significantly less variance in solve times and negligible impact on performance arising from the use of outer approximations.