James Fitzpatrick
Learning to Sparsify Travelling Salesman Problem Instances
Apr 19, 2021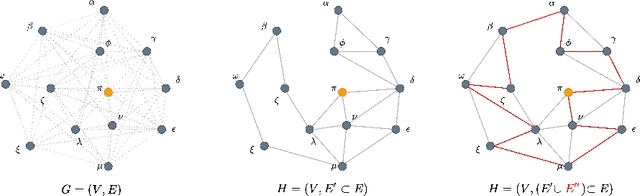


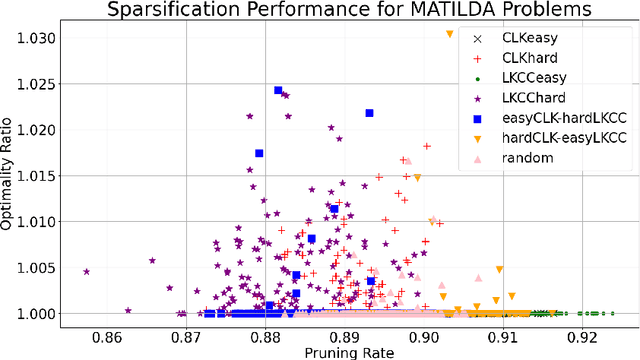
Abstract:In order to deal with the high development time of exact and approximation algorithms for NP-hard combinatorial optimisation problems and the high running time of exact solvers, deep learning techniques have been used in recent years as an end-to-end approach to find solutions. However, there are issues of representation, generalisation, complex architectures, interpretability of models for mathematical analysis etc. using deep learning techniques. As a compromise, machine learning can be used to improve the run time performance of exact algorithms in a matheuristics framework. In this paper, we use a pruning heuristic leveraging machine learning as a pre-processing step followed by an exact Integer Programming approach. We apply this approach to sparsify instances of the classical travelling salesman problem. Our approach learns which edges in the underlying graph are unlikely to belong to an optimal solution and removes them, thus sparsifying the graph and significantly reducing the number of decision variables. We use carefully selected features derived from linear programming relaxation, cutting planes exploration, minimum-weight spanning tree heuristics and various other local and statistical analysis of the graph. Our learning approach requires very little training data and is amenable to mathematical analysis. We demonstrate that our approach can reliably prune a large fraction of the variables in TSP instances from TSPLIB/MATILDA (>85%$) while preserving most of the optimal tour edges. Our approach can successfully prune problem instances even if they lie outside the training distribution, resulting in small optimality gaps between the pruned and original problems in most cases. Using our learning technique, we discover novel heuristics for sparsifying TSP instances, that may be of independent interest for variants of the vehicle routing problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge