Neuromorphic Online Clustering and Its Application to Spike Sorting

Active dendrites are the basis for biologically plausible neural networks possessing many desirable features of the biological brain including flexibility, dynamic adaptability, and energy efficiency. A formulation for active dendrites using the notational language of conventional machine learning is put forward as an alternative to a spiking neuron formulation. Based on this formulation, neuromorphic dendrites are developed as basic neural building blocks capable of dynamic online clustering. Features and capabilities of neuromorphic dendrites are demonstrated via a benchmark drawn from experimental neuroscience: spike sorting. Spike sorting takes inputs from electrical probes implanted in neural tissue, detects voltage spikes (action potentials) emitted by neurons, and attempts to sort the spikes according to the neuron that emitted them. Many spike sorting methods form clusters based on the shapes of action potential waveforms, under the assumption that spikes emitted by a given neuron have similar shapes and will therefore map to the same cluster. Using a stream of synthetic spike shapes, the accuracy of the proposed dendrite is compared with the more compute-intensive, offline k-means clustering approach. Overall, the dendrite outperforms k-means and has the advantage of requiring only a single pass through the input stream, learning as it goes. The capabilities of the neuromorphic dendrite are demonstrated for a number of scenarios including dynamic changes in the input stream, differing neuron spike rates, and varying neuron counts.

Implementing Online Reinforcement Learning with Clustering Neural Networks

An agent employing reinforcement learning takes inputs (state variables) from an environment and performs actions that affect the environment in order to achieve some objective. Rewards (positive or negative) guide the agent toward improved future actions. This paper builds on prior clustering neural network research by constructing an agent with biologically plausible neo-Hebbian three-factor synaptic learning rules, with a reward signal as the third factor (in addition to pre- and post-synaptic spikes). The classic cart-pole problem (balancing an inverted pendulum) is used as a running example throughout the exposition. Simulation results demonstrate the efficacy of the approach, and the proposed method may eventually serve as a low-level component of a more general method.

A Macrocolumn Architecture Implemented with Temporal (Spiking) Neurons

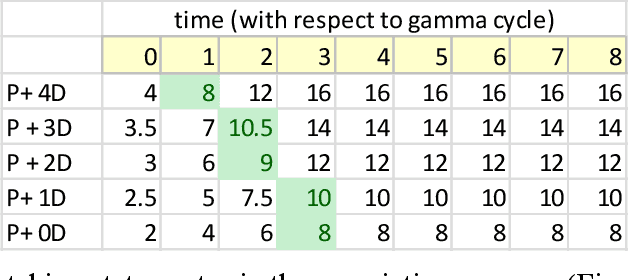
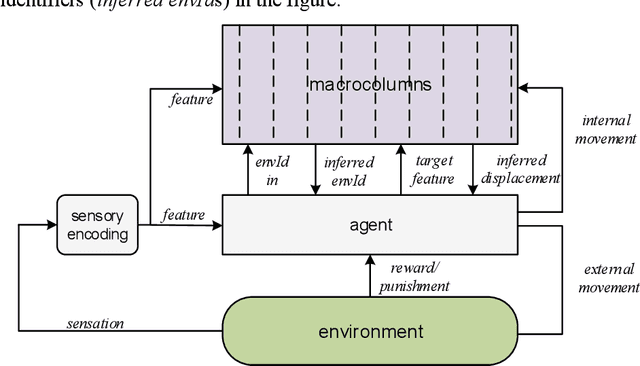
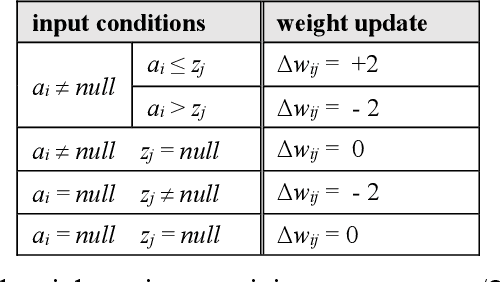
With the long-term goal of reverse-architecting the computational brain from the bottom up, the focus of this document is the macrocolumn abstraction layer. A basic macrocolumn architecture is developed by first describing its operation with a state machine model. Then state machine functions are implemented with spiking neurons that support temporal computation. The neuron model is based on active spiking dendrites and mirrors the Hawkins/Numenta neuron model. The architecture is demonstrated with a research benchmark in which an agent uses a macrocolumn to first learn and then navigate 2-d environments containing randomly placed features. Environments are represented in the macrocolumn as labeled directed graphs where edges connect features and labels indicate the relative displacements between them.

Implementing Online Reinforcement Learning with Temporal Neural Networks

A Temporal Neural Network (TNN) architecture for implementing efficient online reinforcement learning is proposed and studied via simulation. The proposed T-learning system is composed of a frontend TNN that implements online unsupervised clustering and a backend TNN that implements online reinforcement learning. The reinforcement learning paradigm employs biologically plausible neo-Hebbian three-factor learning rules. As a working example, a prototype implementation of the cart-pole problem (balancing an inverted pendulum) is studied via simulation.

Temporal Computer Organization

This document is focused on computing systems implemented in technologies that communicate and compute with temporal transients. Although described in general terms, implementations of spiking neural networks are of primary interest. As background, an algebra for constructing temporal networks is summarized. Then, a system organization consisting of synchronized segments is described. The segments are feedforward internally with feedback between segments. A synchronizing clock resets network segments at the end of each computation step or cycle. In its basic form, the synchronizing clock merely performs a reset function. In the context of neural networks, this satisfies biological plausibility. However, functional completeness is restricted. This restriction is removed by allowing use of the synchronizing clock as an additional function input that acts as a temporal reference value.

A Microarchitecture Implementation Framework for Online Learning with Temporal Neural Networks

Temporal Neural Networks (TNNs) are spiking neural networks that use time as a resource to represent and process information, similar to the mammalian neocortex. In contrast to compute-intensive deep neural networks that employ separate training and inference phases, TNNs are capable of extremely efficient online incremental/continual learning and are excellent candidates for building edge-native sensory processing units. This work proposes a microarchitecture framework for implementing TNNs using standard CMOS. Gate-level implementations of three key building blocks are presented: 1) multi-synapse neurons, 2) multi-neuron columns, and 3) unsupervised and supervised online learning algorithms based on Spike Timing Dependent Plasticity (STDP). The proposed microarchitecture is embodied in a set of characteristic scaling equations for assessing the gate count, area, delay and power for any TNN design. Post-synthesis results (in 45nm CMOS) for the proposed designs are presented, and their online incremental learning capability is demonstrated.

A Temporal Neural Network Architecture for Online Learning

A long-standing proposition is that by emulating the operation of the brain's neocortex, a spiking neural network (SNN) can achieve similar desirable features: flexible learning, speed, and efficiency. Temporal neural networks (TNNs) are SNNs that communicate and process information encoded as relative spike times (in contrast to spike rates). A TNN architecture is proposed, and, as a proof-of-concept, TNN operation is demonstrated within the larger context of online supervised classification. First, through unsupervised learning, a TNN partitions input patterns into clusters based on similarity. The TNN then passes a cluster identifier to a simple online supervised decoder which finishes the classification task. The TNN learning process adjusts synaptic weights by using only signals local to each synapse, and clustering behavior emerges globally. The system architecture is described at an abstraction level analogous to the gate and register transfer levels in conventional digital design. Besides features of the overall architecture, several TNN components are new to this work. Although not addressed directly, the overall research objective is a direct hardware implementation of TNNs. Consequently, all the architecture elements are simple, and processing is done at very low precision. Importantly, low precision leads to very fast learning times. Simulation results using the time-honored MNIST dataset demonstrate learning times at least an order of magnitude faster than other online approaches while providing similar error rates.

Direct CMOS Implementation of Neuromorphic Temporal Neural Networks for Sensory Processing

Temporal Neural Networks (TNNs) use time as a resource to represent and process information, mimicking the behavior of the mammalian neocortex. This work focuses on implementing TNNs using off-the-shelf digital CMOS technology. A microarchitecture framework is introduced with a hierarchy of building blocks including: multi-neuron columns, multi-column layers, and multi-layer TNNs. We present the direct CMOS gate-level implementation of the multi-neuron column model as the key building block for TNNs. Post-synthesis results are obtained using Synopsys tools and the 45 nm CMOS standard cell library. The TNN microarchitecture framework is embodied in a set of characteristic equations for assessing the total gate count, die area, compute time, and power consumption for any TNN design. We develop a multi-layer TNN prototype of 32M gates. In 7 nm CMOS process, it consumes only 1.54 mm^2 die area and 7.26 mW power and can process 28x28 images at 107M FPS (9.34 ns per image). We evaluate the prototype's performance and complexity relative to a recent state-of-the-art TNN model.

A Neuromorphic Paradigm for Online Unsupervised Clustering

A computational paradigm based on neuroscientific concepts is proposed and shown to be capable of online unsupervised clustering. Because it is an online method, it is readily amenable to streaming realtime applications and is capable of dynamically adjusting to macro-level input changes. All operations, both training and inference, are localized and efficient. The paradigm is implemented as a cognitive column that incorporates five key elements: 1) temporal coding, 2) an excitatory neuron model for inference, 3) winner-take-all inhibition, 4) a column architecture that combines excitation and inhibition, 5) localized training via spike timing de-pendent plasticity (STDP). These elements are described and discussed, and a prototype column is given. The prototype column is simulated with a semi-synthetic benchmark and is shown to have performance characteristics on par with classic k-means. Simulations reveal the inner operation and capabilities of the column with emphasis on excitatory neuron response functions and STDP implementations.

(Newtonian) Space-Time Algebra

The space-time (s-t) algebra provides a mathematical model for communication and computation using values encoded as events in discretized linear (Newtonian) time. Consequently, the input-output behavior of s-t algebra and implemented functions are consistent with the flow of time. The s-t algebra and functions are formally defined. A network design framework for s-t functions is described, and the design of temporal neural networks, a form of spiking neural networks, is discussed as an extended case study. Finally, the relationship with Allen's interval algebra is briefly discussed.