James E. Galagan
Learning modular structures from network data and node variables
May 11, 2014
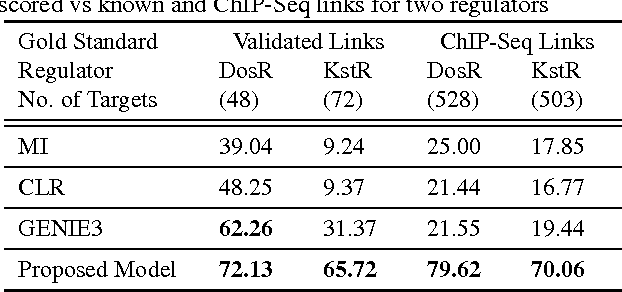
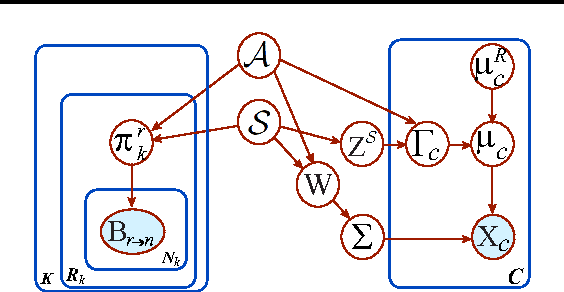
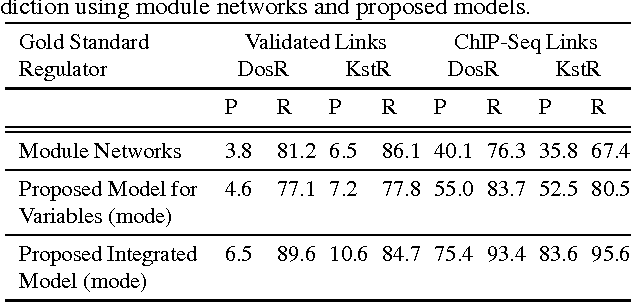
Abstract:A standard technique for understanding underlying dependency structures among a set of variables posits a shared conditional probability distribution for the variables measured on individuals within a group. This approach is often referred to as module networks, where individuals are represented by nodes in a network, groups are termed modules, and the focus is on estimating the network structure among modules. However, estimation solely from node-specific variables can lead to spurious dependencies, and unverifiable structural assumptions are often used for regularization. Here, we propose an extended model that leverages direct observations about the network in addition to node-specific variables. By integrating complementary data types, we avoid the need for structural assumptions. We illustrate theoretical and practical significance of the model and develop a reversible-jump MCMC learning procedure for learning modules and model parameters. We demonstrate the method accuracy in predicting modular structures from synthetic data and capability to learn influence structures in twitter data and regulatory modules in the Mycobacterium tuberculosis gene regulatory network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge