On-the-fly Strategy Adaptation for ad-hoc Agent Coordination

Training agents in cooperative settings offers the promise of AI agents able to interact effectively with humans (and other agents) in the real world. Multi-agent reinforcement learning (MARL) has the potential to achieve this goal, demonstrating success in a series of challenging problems. However, whilst these advances are significant, the vast majority of focus has been on the self-play paradigm. This often results in a coordination problem, caused by agents learning to make use of arbitrary conventions when playing with themselves. This means that even the strongest self-play agents may have very low cross-play with other agents, including other initializations of the same algorithm. In this paper we propose to solve this problem by adapting agent strategies on the fly, using a posterior belief over the other agents' strategy. Concretely, we consider the problem of selecting a strategy from a finite set of previously trained agents, to play with an unknown partner. We propose an extension of the classic statistical technique, Gibbs sampling, to update beliefs about other agents and obtain close to optimal ad-hoc performance. Despite its simplicity, our method is able to achieve strong cross-play with unseen partners in the challenging card game of Hanabi, achieving successful ad-hoc coordination without knowledge of the partner's strategy a priori.

Mixture Density Conditional Generative Adversarial Network Models (MD-CGAN)

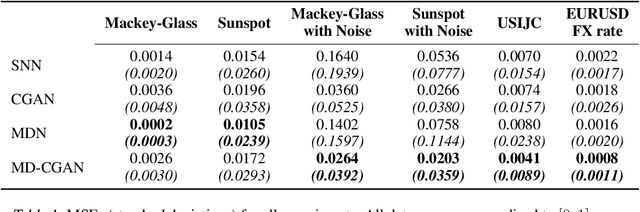
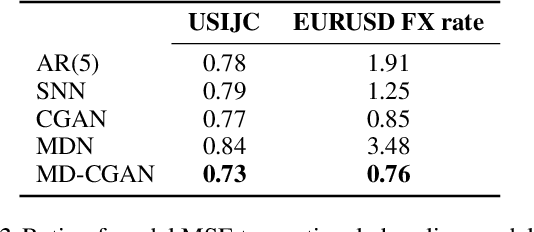
Generative Adversarial Networks (GANs) have gained significant attention in recent years, with particularly impressive applications highlighted in computer vision. In this work, we present a Mixture Density Conditional Generative Adversarial Model (MD-CGAN), where the generator is a Gaussian mixture model, with a focus on time series forecasting. Compared to examples in vision, there have been more limited applications of GAN models to time series. We show that our model is capable of estimating a probabilistic posterior distribution over forecasts and that, in comparison to a set of benchmark methods, the MD-CGAN model performs well, particularly in situations where noise is a significant in the time series. Further, by using a Gaussian mixture model that allows for a flexible number of mixture coefficients, the MD-CGAN offers posterior distributions that are non-Gaussian.