Mixture Density Conditional Generative Adversarial Network Models (MD-CGAN)

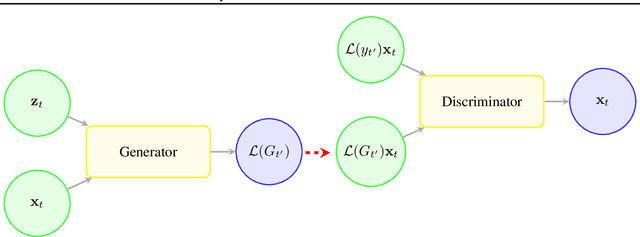
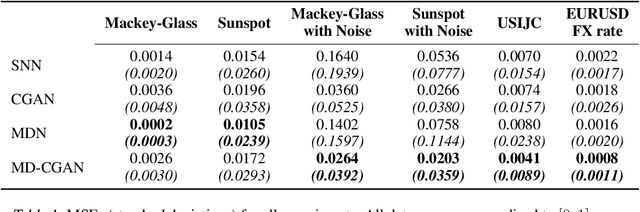
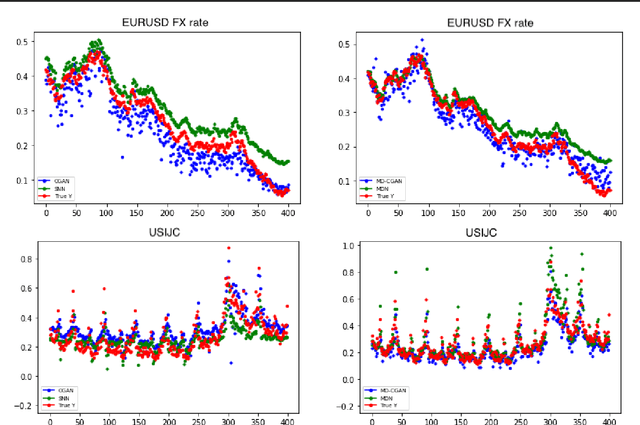
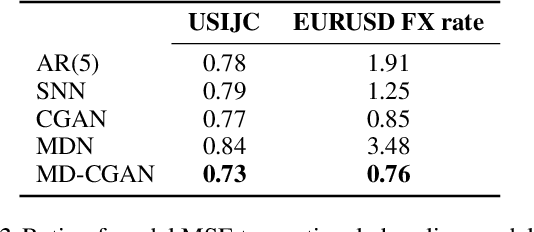
Generative Adversarial Networks (GANs) have gained significant attention in recent years, with particularly impressive applications highlighted in computer vision. In this work, we present a Mixture Density Conditional Generative Adversarial Model (MD-CGAN), where the generator is a Gaussian mixture model, with a focus on time series forecasting. Compared to examples in vision, there have been more limited applications of GAN models to time series. We show that our model is capable of estimating a probabilistic posterior distribution over forecasts and that, in comparison to a set of benchmark methods, the MD-CGAN model performs well, particularly in situations where noise is a significant in the time series. Further, by using a Gaussian mixture model that allows for a flexible number of mixture coefficients, the MD-CGAN offers posterior distributions that are non-Gaussian.