Hyperspectral Unmixing using Iterative, Sparse and Ensambling Approaches for Large Spectral Libraries Applied to Soils and Minerals

Unmixing is a fundamental process in hyperspectral image processing in which the materials present in a mixed pixel are determined based on the spectra of candidate materials and the pixel spectrum. Practical and general utility requires a large spectral library with sample measurements covering the full variation in each candidate material as well as a sufficiently varied collection of potential materials. However, any spectral library with more spectra than bands will lead to an ill-posed inversion problem when using classical least-squares regression-based unmixing methods. Moreover, for numerical and dimensionality reasons, libraries with over 10 or 20 spectra behave computationally as though they are ill-posed. In current practice, unmixing is often applied to imagery using manually-selected materials or image endmembers. General unmixing of a spectrum from an unknown material with a large spectral library requires some form of sparse regression; regression where only a small number of coefficients are nonzero. This requires a trade-off between goodness-of-fit and model size. In this study we compare variations of two sparse regression techniques, focusing on the relationship between structure and chemistry of materials and the accuracy of the various models for identifying the correct mixture of materials present. Specifically, we examine LASSO regression and ElasticNet in contrast with variations of iterative feature selection, Bayesian Model Averaging (BMA), and quadratic BMA (BMA-Q) -- incorporating LASSO regression and ElasticNet as their base model. To evaluate the the effectiveness of these methods, we consider the molecular composition similarities and differences of substances selected in the models compared to the ground truth.

Spectral Unmixing Comparison with Sparse, Iterative and Mixed Integer Programming Models

Hyperspectral unmixing is the analytical process of determining the pure materials and estimating the proportions of such materials composed within an observed mixed pixel spectrum. We can unmix mixed pixel spectra using linear and nonlinear mixture models. Ordinary least squares (OLS) regression serves as the foundation for many linear mixture models employed in Hyperspectral Image analysis. Though variations of OLS are implemented, studies rarely address the underlying assumptions that affect results. This paper provides an in depth discussion on the assumptions inherently endorsed by the application of OLS regression. We also examine variations of OLS models stemming from highly effective approaches in spectral unmixing -- sparse regression, iterative feature search strategies and Mathematical programming. These variations are compared to a novel unmixing approach called HySUDeB. We evaluated each approach's performance by computing the average error and precision of each model. Additionally, we provide a taxonomy of the molecular structure of each mineral to derive further understanding into the detection of the target materials.

Theoretical and Practical Progress in Hyperspectral Pixel Unmixing with Large Spectral Libraries from a Sparse Perspective

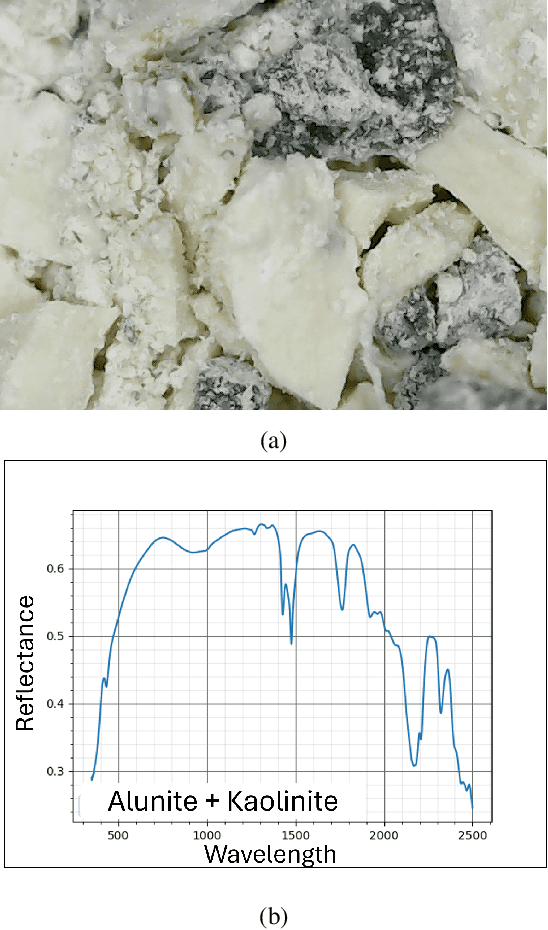
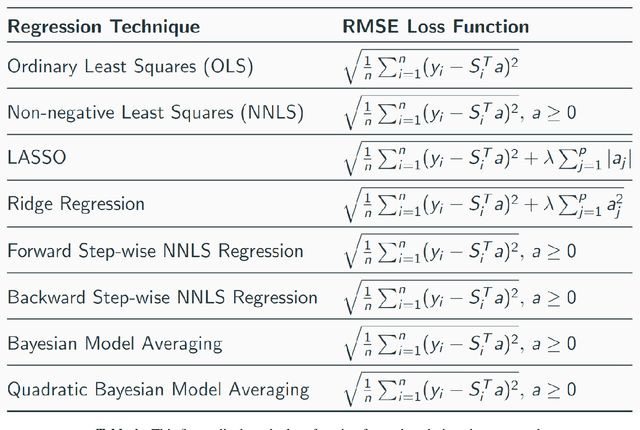
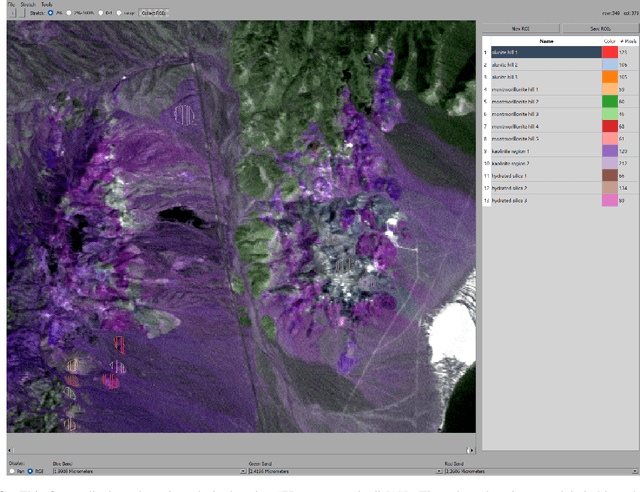
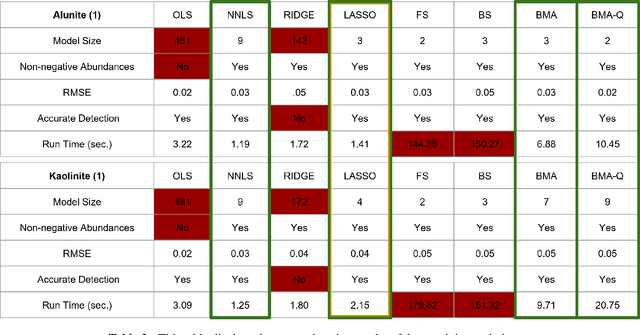
Hyperspectral unmixing is the process of determining the presence of individual materials and their respective abundances from an observed pixel spectrum. Unmixing is a fundamental process in hyperspectral image analysis, and is growing in importance as increasingly large spectral libraries are created and used. Unmixing is typically done with ordinary least squares (OLS) regression. However, unmixing with large spectral libraries where the materials present in a pixel are not a priori known, solving for the coefficients in OLS requires inverting a non-invertible matrix from a large spectral library. A number of regression methods are available that can produce a numerical solution using regularization, but with considerably varied effectiveness. Also, simple methods that are unpopular in the statistics literature (i.e. step-wise regression) are used with some level of effectiveness in hyperspectral analysis. In this paper, we provide a thorough performance evaluation of the methods considered, evaluating methods based on how often they select the correct materials in the models. Investigated methods include ordinary least squares regression, non-negative least squares regression, ridge regression, lasso regression, step-wise regression and Bayesian model averaging. We evaluated these unmixing approaches using multiple criteria: incorporation of non-negative abundances, model size, accurate mineral detection and root mean squared error (RMSE). We provide a taxonomy of the regression methods, showing that most methods can be understood as Bayesian methods with specific priors. We conclude that methods that can be derived with priors that correspond to the phenomenology of hyperspectral imagery outperform those with priors that are optimal for prediction performance under the assumptions of ordinary least squares linear regression.

Fairness and Privacy in Federated Learning and Their Implications in Healthcare

Currently, many contexts exist where distributed learning is difficult or otherwise constrained by security and communication limitations. One common domain where this is a consideration is in Healthcare where data is often governed by data-use-ordinances like HIPAA. On the other hand, larger sample sizes and shared data models are necessary to allow models to better generalize on account of the potential for more variability and balancing underrepresented classes. Federated learning is a type of distributed learning model that allows data to be trained in a decentralized manner. This, in turn, addresses data security, privacy, and vulnerability considerations as data itself is not shared across a given learning network nodes. Three main challenges to federated learning include node data is not independent and identically distributed (iid), clients requiring high levels of communication overhead between peers, and there is the heterogeneity of different clients within a network with respect to dataset bias and size. As the field has grown, the notion of fairness in federated learning has also been introduced through novel implementations. Fairness approaches differ from the standard form of federated learning and also have distinct challenges and considerations for the healthcare domain. This paper endeavors to outline the typical lifecycle of fair federated learning in research as well as provide an updated taxonomy to account for the current state of fairness in implementations. Lastly, this paper provides added insight into the implications and challenges of implementing and supporting fairness in federated learning in the healthcare domain.